problem
stringlengths 1
13.6k
| solution
stringlengths 0
18.5k
⌀ | answer
stringlengths 0
575
⌀ | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 8
values | synthetic
bool 1
class | __index_level_0__
int64 0
742k
|
|---|---|---|---|---|---|---|---|---|---|
G2 For a fixed triangle $A B C$ we choose a point $M$ on the ray $C A$ (after $A$ ), a point $N$ on the ray $A B$ (after $B$ ) and a point $P$ on the ray $B C$ (after $C$ ) in a way such that $A M-B C=B N-A C=C P-A B$. Prove that the angles of triangle $M N P$ do not depend on the choice of $M, N, P$.
|
## Solution
Consider the points $M^{\prime}$ on the ray $B A$ (after $A$ ), $N^{\prime}$ on the ray $C B$ (after $B$ ) and $P^{\prime}$ on the ray $A C$ (after $C$ ), so that $A M=A M^{\prime}, B N=B N^{\prime}, C P=C P^{\prime}$. Since $A M-B C=B N-A C=B N^{\prime}-A C$, we get $C M=A C+A M=B C+B N^{\prime}=C N^{\prime}$. Thus triangle $M C N^{\prime}$ is isosceles, so the perpendicular bisector of $\left[M N^{\prime}\right]$ bisects angle $A C B$ and hence passes through the incenter $I$ of triangle $A B C$. Arguing similarly, we may conclude that $I$ lies also on the perpendicular bisectors of $\left[N P^{\prime}\right]$ and $\left[P M^{\prime}\right]$. On the other side, $I$ clearly lies on the perpendicular bisectors of $\left[M M^{\prime}\right],\left[N N^{\prime}\right]$ and $\left[P P^{\prime}\right]$. Thus the hexagon $M^{\prime} M N^{\prime} N P^{\prime} P$ is cyclic. Then angle $P M N$ equals angle $P N^{\prime} N$, which measures $90^{\circ}-\frac{\beta}{2}$ (the angles of triangle $A B C$ are $\alpha, \beta, \gamma$ ). In the same way angle $M N P$ measures $90^{\circ}-\frac{\gamma}{2}$ and angle $M P N$ measures $90^{\circ}-\frac{\alpha}{2}$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 321
|
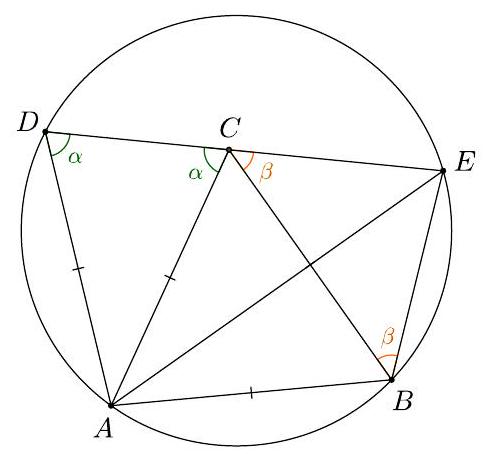
G3 The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
## Solution
As $A D=A C, \triangle C D A$ is isosceles. If $\varangle A D C=\varangle A C D=\alpha$ and $\varangle B C E=\beta$, then $\beta=120^{\circ}-\alpha$. The quadrilateral $A B E D$ is cyclic, so $\varangle A B E=180^{\circ}-\alpha$. Then $\varangle C B E=$ $120^{\circ}-\alpha$ so $\varangle C B E=\beta$. Thus $\triangle C B E$ is isosceles, so $A E$ is the perpendicular bisector of $B C$, so it bisects $\varangle B A C$. Now the arc $B E$ is intercepted by a $30^{\circ}$ inscribed angle, so it measures $60^{\circ}$. Then $B E$ equals the radius of $k$, namely 1 . Hence $C E=B E=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 322
|
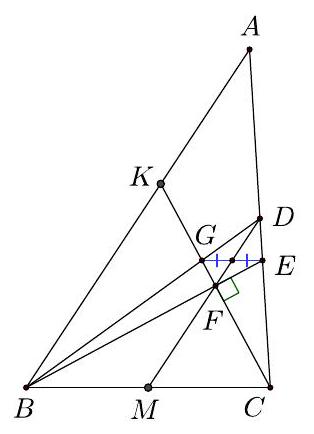
G4 Let $A B C$ be a triangle, $(B C<A B)$. The line $\ell$ passing trough the vertices $C$ and orthogonal to the angle bisector $B E$ of $\angle B$, meets $B E$ and the median $B D$ of the side $A C$ at points $F$ and $G$, respectively. Prove that segment $D F$ bisect the segment $E G$.
|
## Solution
Let $C F \cap A B=\{K\}$ and $D F \cap B C=\{M\}$. Since $B F \perp K C$ and $B F$ is angle bisector of $\varangle K B C$, we have that $\triangle K B C$ is isosceles i.e. $B K=B C$, also $F$ is midpoint of $K C$. Hence $D F$ is midline for $\triangle A C K$ i.e. $D F \| A K$, from where it is clear that $M$ is a midpoint of $B C$.
We will prove that $G E \| B C$. It is sufficient to show $\frac{B G}{G D}=\frac{C E}{E D}$. From $D F \| A K$ and $D F=\frac{A K}{2}$ we have
$$
\frac{B G}{G D}=\frac{B K}{D F}=\frac{2 B K}{A K}
$$
Also
$$
\begin{gathered}
\frac{C E}{D E}=\frac{C D-D E}{D E}=\frac{C D}{D E}-1=\frac{A D}{D E}-1=\frac{A E-D E}{D E}-1=\frac{A E}{D E}-2= \\
=\frac{A B}{D F}-2=\frac{A K+B K}{\frac{A K}{2}}-2=2+2 \frac{B K}{A K}-2=\frac{2 B K}{A K}
\end{gathered}
$$
From (1) and (2) we have $\frac{B G}{G D}=\frac{C E}{E D}$, so $G E \| B C$, as $M$ is the midpoint of $B C$, it follows that the segment $D F$, bisects the segment $G E$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 323
|
G5 Is it possible to cover a given square with a few congruent right-angled triangles with acute angle equal to $30^{\circ}$ ? (The triangles may not overlap and may not exceed the margins of the square.)
|
## Solution
We will prove that desired covering is impossible.
Let assume the opposite i.e. a square with side length $a$, can be tiled with $k$ congruent right angled triangles, whose sides are of lengths $b, b \sqrt{3}$ and $2 b$.
Then the area of such a triangle is $\frac{b^{2} \sqrt{3}}{2}$.
And the area of the square is
$$
S_{s q}=k b^{2} \frac{\sqrt{3}}{2}
$$
Furthermore, the length of the side of the square, $a$, is obtained by the contribution of an integer number of length $b, 2 b$ and $b \sqrt{3}$, hence
$$
a=m b \sqrt{3}+n b
$$
where $m, n \in \mathbb{N} \cup\{0\}$, and at least one of the numbers $m$ and $n$ is different from zero. So the area of the square is
$$
S_{s q}=a^{2}=(m b \sqrt{3}+n b)^{2}=b^{2}\left(3 m^{2}+n^{2}+2 \sqrt{3} m n\right)
$$
Now because of (1) and (2) it follows $3 m^{2}+n^{2}+2 \sqrt{3} m n=k \frac{\sqrt{3}}{2}$ i.e.
$$
6 m^{2}+2 n^{2}=(k-4 m n) \sqrt{3}
$$
Because of $3 m^{2}+n^{2} \neq 0$ and from the equality (3) it follows $4 m n \neq k$. Using once more (3), we get
$$
\sqrt{3}=\frac{6 m^{2}+2 n^{2}}{k-4 m n}
$$
which contradicts at the fact that $\sqrt{3}$ is irrational, because $\frac{6 m^{2}+2 n^{2}}{k-4 m n}$ is a rational number.
Finally, we have obtained a contradiction, which proves that the desired covering is impossible.
## Remark.
This problem has been given in Russian Mathematical Olympiad 1993 - 1995 for 9-th Grade.
|
proof
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 324
|
G6 Let $A B C$ be a triangle with $A<90^{\circ}$. Outside of a triangle we consider isosceles triangles $A B E$ and $A C Z$ with bases $A B$ and $A C$, respectively. If the midpoint $D$ of the side $B C$ is such that $D E \perp D Z$ and $E Z=2 \cdot E D$, prove that $\widehat{A E B}=2 \cdot \widehat{A Z C}$.
|
## Solution
Since $D$ is the midpoint of the side $B C$, in the extension of the line segment $Z D$ we take a point $H$ such that $Z D=D H$. Then the quadrilateral $B H C Z$ is parallelogram and therefore we have
$$
B H=Z C=Z A
$$
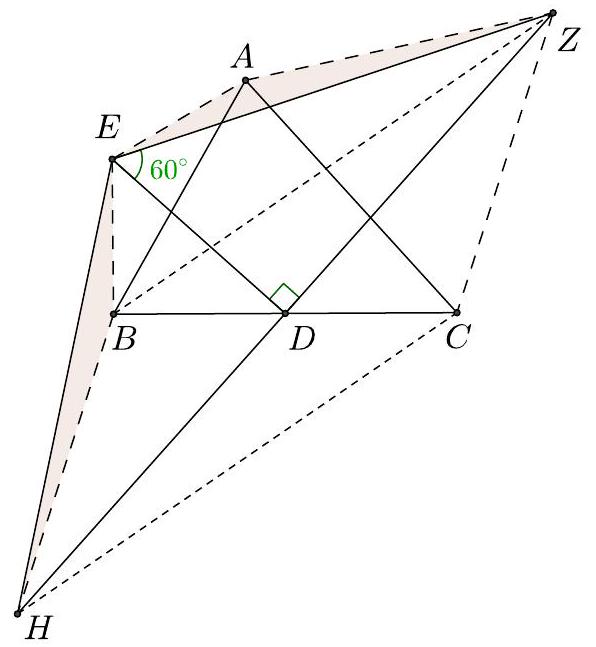
Also from the isosceles triangle $A B E$ we get
$$
B E=A E
$$
Since $D E \perp D Z, E D$ is altitude and median of the triangle $E Z H$ and so this triangle is isosceles with
$$
E H=E Z
$$
From (1), (2) and (3) we conclude that the triangles $B E H$ and $A E Z$ are equal. Therefore they have also
$$
\widehat{B E H}=\widehat{A E Z}, \widehat{E B H}=\widehat{E A Z} \text { and } \widehat{E H B}=\widehat{A Z E}
$$
Putting $\widehat{E B A}=\widehat{E A B}=\omega, \widehat{Z A C}=\widehat{Z C A}=\varphi$, then we have $\widehat{C B H}=\widehat{B C Z}=\widehat{C}+\varphi$, and therefore from the equality $\widehat{E B H}=\widehat{E A Z}$ we receive:
$$
\begin{gathered}
360^{\circ}-\widehat{E B A}-\widehat{B}-\widehat{C B H}=\widehat{E A B}+\widehat{A}+\widehat{Z A C} \\
\Rightarrow 360^{\circ}-\widehat{B}-\omega-\varphi-\widehat{C}=\omega+\widehat{A}+\varphi \\
\Rightarrow 2(\omega+\varphi)=360^{\circ}-(\widehat{A}+\widehat{B}+\widehat{C}) \\
\Rightarrow \omega+\varphi=90^{\circ} \\
\Rightarrow \frac{180^{\circ}-\widehat{A E B}}{2}+\frac{180^{\circ}-\widehat{A Z C}}{2}=90^{\circ} \\
\Rightarrow \widehat{A E B}+\widehat{A Z C}=180^{\circ}
\end{gathered}
$$
From the supposition $E Z=2 \cdot E D$, we get that the right triangle $Z E H$ has $\widehat{E Z D}=30^{\circ}$ and $\widehat{Z E D}=60^{\circ}$. Thus we have $\widehat{Z E H}=120^{\circ}$.
However, since we have proved that $\widehat{B E H}=\widehat{A E Z}$, we get that
$$
\widehat{A E B}=\widehat{A E Z}+\widehat{Z E B}=\widehat{Z E B}+\widehat{B E H}=\widehat{Z E H}=120^{\circ}
$$
From (5) and (6) we obtain that $\widehat{A Z C}=60^{\circ}$ and thus $\widehat{A E B}=2 \cdot \widehat{A Z C}$.
|
\widehat{AEB}=2\cdot\widehat{AZC}
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 325
|
G7 Let $A B C$ be an isosceles triangle with $A C=B C$. The point $D$ lies on the side $A B$ such that the semicircle with diameter $[B D]$ and center $O$ is tangent to the side $A C$ in the point $P$ and intersects the side $B C$ at the point $Q$. The radius $O P$ intersects the chord $D Q$ at the point $E$ such that $5 \cdot P E=3 \cdot D E$. Find the ratio $\frac{A B}{B C}$.
|
## Solution
We denote $O P=O D=O B=R, A C=B C=b$ and $A B=2 a$. Because $O P \perp A C$ and $D Q \perp B C$, then the right triangles $A P O$ and $B Q D$ are similar and $\varangle B D Q=\varangle A O P$. So, the triangle $D E O$ is isosceles with $D E=O E$. It follows that
$$
\frac{P E}{D E}=\frac{P E}{O E}=\frac{3}{5}
$$
Let $F$ and $G$ are the orthogonal projections of the points $E$ and $P$ respectively on the side $A B$ and $M$ is the midpoint of the side $[A B]$. The triangles $O F E, O G P, O P A$ and $C M A$ are similar. We obtain the following relations
$$
\frac{O F}{O E}=\frac{O G}{O P}=\frac{C M}{A C}=\frac{O P}{O A}
$$
But $C M=\sqrt{b^{2}-a^{2}}$ and we have $O G=\frac{R}{b} \cdot \sqrt{b^{2}-a^{2}}$. In isosceles triangle $D E O$ the point $F$ is the midpoint of the radius $D O$. So, $O F=R / 2$. By using Thales' theorem we obtain
$$
\frac{3}{5}=\frac{P E}{O E}=\frac{G F}{O F}=\frac{O G-O F}{O F}=\frac{O G}{O F}-1=2 \cdot \sqrt{1-\left(\frac{a}{b}\right)^{2}}-1
$$
From the last relations it is easy to obtain that $\frac{a}{b}=\frac{3}{5}$ and $\frac{A B}{B C}=\frac{6}{5}$.
The problem is solved.
|
\frac{6}{5}
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 326
|
G8 The side lengths of a parallelogram are $a, b$ and diagonals have lengths $x$ and $y$, Knowing that $a b=\frac{x y}{2}$, show that
$$
a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}} \text { or } a=\frac{y}{\sqrt{2}}, b=\frac{x}{\sqrt{2}}
$$
|
## Solution 1.
Let us consider a parallelogram $A B C D$, with $A B=a, B C=b, A C=x, B D=y$, $\widehat{A O D}=\theta$.
For the area of $A B C D$ we know $(A B C D)=a b \sin A$.
But it is also true that $(A B C D)=4(A O D)=4 \cdot \frac{O A \cdot O D}{2} \sin \theta=2 O A \cdot O D \sin \theta=$ $=2 \cdot \frac{x}{2} \cdot \frac{y}{2} \sin \theta=\frac{x y}{2} \sin \theta$. So $a b \sin A=\frac{x y}{2} \sin \theta$ and since $a b=\frac{x y}{2}$ by hypothesis, we get
$$
\sin A=\sin \theta
$$
Thus
$$
\theta=\widehat{A} \text { or } \theta=180^{\circ}-\widehat{A}=\widehat{B}
$$
If $\theta=A$ then (see Figure below) $A_{2}+B_{1}=A_{1}+A_{2}$, so $B_{1}=A_{1}$ which implies that $A D$ is tangent to the circumcircle of triangle $O A B$. So
$$
D A^{2}=D O \cdot D B \Rightarrow b^{2}=\frac{y}{2} \cdot y \Rightarrow b=\frac{y}{\sqrt{2}}
$$
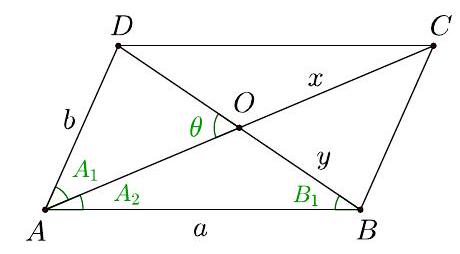
Then by $a b=\frac{x y}{2}$ we get $a=\frac{x}{\sqrt{2}}$.
If $\theta=B$ we similarly get $a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}}$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 327
|
G9 Let $O$ be a point inside the parallelogram $A B C D$ such that
$$
\angle A O B+\angle C O D=\angle B O C+\angle C O D
$$
Prove that there exists a circle $k$ tangent to the circumscribed circles of the triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$.
|
## Solution
From given condition it is clear that $\varangle A O B+\varangle C O D=\varangle B O C+\varangle A O D=180^{\circ}$.
Let $E$ be a point such that $A E=D O$ and $B E=C E$. Clearly, $\triangle A E B \equiv \triangle D O C$ and from that $A E \| D O$ and $B E \| C O$. Also, $\varangle A E B=\varangle C O D$ so $\varangle A O B+\varangle A E B=$ $\varangle A O B+\varangle C O D=180^{\circ}$. Thus, the quadrilateral $A O B E$ is cyclic.
So $\triangle A O B$ and $\triangle A E B$ the same circumcircle, therefor the circumcircles of the triangles $\triangle A O B$ and $\triangle C O D$ have the same radius.
Also, $A E \| D O$ and $A E=D O$ gives $A E O D$ is parallelogram and $\triangle A O D \equiv \triangle O A E$. So $\triangle A O B, \triangle C O D$ and $\triangle D O A$ has the same radius of their circumcircle (the radius of the cyclic quadrilateral $A E B O)$. Analogously, triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$ has same radius $R$.
Obviously, the circle with center $O$ and radius $2 R$ is externally tangent to each of these circles, so this will be the circle $k$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 328
|
G10 Let $\Gamma$ be a circle of center $O$, and $\delta$ be a line in the plane of $\Gamma$, not intersecting it. Denote by $A$ the foot of the perpendicular from $O$ onto $\delta$, and let $M$ be a (variable) point on $\Gamma$. Denote by $\gamma$ the circle of diameter $A M$, by $X$ the (other than $M$ ) intersection point of $\gamma$ and $\Gamma$, and by $Y$ the (other than $A$ ) intersection point of $\gamma$ and $\delta$. Prove that the line $X Y$ passes through a fixed point.
|
## Solution
Consider the line $\rho$ tangent to $\gamma$ at $A$, and take the points $\{K\}=A M \cap X Y,\{L\}=$ $\rho \cap X M$, and $\{F\}=O A \cap X Y$.
(Remark: Moving $M$ into its reflection with respect to the line $O A$ will move $X Y$ into its reflection with respect to $O A$. These old and the new $X Y$ meet on $O A$, hence it should be clear that the fixed point mult be $F$.)
Since $\varangle L M A=\varangle F Y A$ and $\varangle Y A F=\varangle L A M=90^{\circ}$, it follows that triangles $F A Y$ and $L A M$ are similar, therefore $\varangle A F Y=\varangle A L M$, hence the quadrilateral $A L X F$ is cyclic. But then $\varangle A F L=\varangle A X L=90^{\circ}$, so $L F \perp A F$, hence $L F \| \delta$.
Now, $\rho$ is the radical axis of circles $\gamma$ and $A$ (consider $A$ as a circle of center $A$ and radius 0 ), while $X M$ is the radical axis of circles $\gamma$ and $\Gamma$, so $L$ is the radical center of the three circle, which means that $L$ lies on the radical axis of circles $\Gamma$ and $A$. From $L F \perp O A$, where $O A$ is the line of the centers of the circles $A$ and $\Gamma$, and $F \in X Y$, it follows that $F$ is (the) fixed point of $X Y$.
(The degenerate two cases when $M \in O A$, where $X \equiv M$ and $Y \equiv A$, also trivially satisfy the conclusion, as then $F \in A M)$.
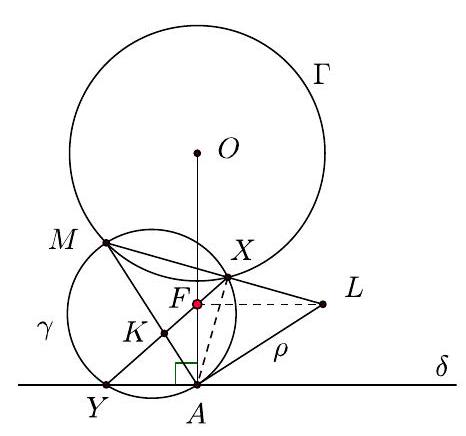
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 329
|
G11 Consider $A B C$ an acute-angled triangle with $A B \neq A C$. Denote by $M$ the midpoint of $B C$, by $D, E$ the feet of the altitudes from $B, C$ respectively and let $P$ be the intersection point of the lines $D E$ and $B C$. The perpendicular from $M$ to $A C$ meets the perpendicular from $C$ to $B C$ at point $R$. Prove that lines $P R$ and $A M$ are perpendicular.
|
Solution
Let $F$ be the foot of the altitude from $A$ and let $S$ be the intersection point of $A M$ and $R C$. As $P C$ is an altitude of the triangle $P R S$, the claim is equivalent to $R M \perp P S$, since the latter implies that $M$ is the orthocenter of $P R S$. Due to $R M \perp A C$, we need to prove that $A C \| P S$, in other words
$$
\frac{M C}{M P}=\frac{M A}{M S}
$$
Notice that $A F \| C S$, so $\frac{M A}{M S}=\frac{M F}{M C}$. Now the claim is reduced to proving $M C^{2}=$ $M F \cdot M P$, a well-known result considering that $A F$ is the polar line of $P$ with respect to circle of radius $M C$ centered at $M$.
The "elementary proof" on the latter result may be obtained as follows: $\frac{P B}{P C}=\frac{F B}{F C}$, using, for instance, Menelaus and Ceva theorems with respect to $A B C$. Cross-multiplying one gets $(P M-x)(F M+x)=(x-F M)(P M+x)$
- $x$ stands for the length of $M C$ - and then $P M \cdot F M=x^{2}$.
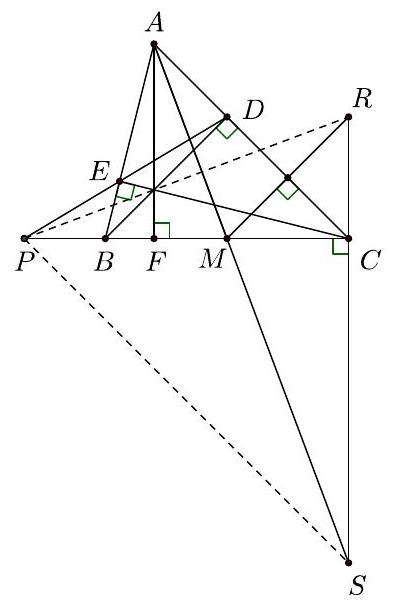
Comment. The proof above holds for both cases $A BA C$; it is for the committee to decide if a contestant is supposed to (even) mention this.
### 2.4 Number Theory
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 330
|
NT1 Find all the positive integers $x$ and $y$ that satisfy the equation
$$
x(x-y)=8 y-7
$$
|
## Solution 1:
The given equation can be written as:
$$
\begin{aligned}
& x(x-y)=8 y-7 \\
& x^{2}+7=y(x+8)
\end{aligned}
$$
Let $x+8=m, m \in \mathbb{N}$. Then we have: $x^{2}+7 \equiv 0(\bmod m)$, and $x^{2}+8 x \equiv 0(\bmod m)$. So we obtain that $8 x-7 \equiv 0(\bmod m) \quad(1)$.
Also we obtain $8 x+8^{2}=8(x+8) \equiv 0(\bmod m) \quad(2)$.
From (1) and $(2)$ we obtain $(8 x+64)-(8 x-7)=71 \equiv 0(\bmod m)$, therefore $m \mid 71$, since 71 is a prime number, we have:
$x+8=1$ or $x+8=71$. The only accepted solution is $x=63$, and from the initial equation we obtain $y=56$.
Therefore the equation has a unique solution, namely $(x, y)=(63,56)$.
|
(x,y)=(63,56)
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 331
|
NT2 Let $n \geq 2$ be a fixed positive integer. An integer will be called " $n$-free" if it is not a multiple of an $n$-th power of a prime. Let $M$ be an infinite set of rational numbers, such that the product of every $n$ elements of $M$ is an $n$-free integer. Prove that $M$ contains only integers.
|
## Solution
We first prove that $M$ can contain only a finite number of non-integers. Suppose that there are infinitely many of them: $\frac{p_{1}}{q_{1}}, \frac{p_{2}}{q_{2}}, \ldots, \frac{p_{k}}{q_{k}}, \ldots$, with $\left(p_{k}, q_{k}\right)=1$ and $q_{k}>1$ for each $k$. Let $\frac{p}{q}=\frac{p_{1} p_{2} \ldots p_{n-1}}{q_{1} q_{2} \ldots q_{n-1}}$, where $(p, q)=1$. For each $i \geq n$, the number $\frac{p}{q} \cdot \frac{p_{i}}{q_{i}}$ is an integer, so $q_{i}$ is a divisor of $p$ (as $q_{i}$ and $p_{i}$ are coprime). But $p$ has a finite set of divisors, so there are $n$ numbers of $M$ with equal denominators. Their product cannot be an integer, a contradiction.
Now suppose that $M$ contains a fraction $\frac{a}{b}$ in lowest terms with $b>1$. Take a prime divisor $p$ of $b$. If we take any $n-1$ integers from $M$, their product with $\frac{a}{b}$ is an integer, so some of them is a multiple of $p$. Therefore there are infinitely many multiples of $p$ in $M$, and the product of $n$ of them is not $n$-free, a contradiction.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 332
|
NT3 Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
|
## Solution
Since $a_{n-1} \equiv s\left(a_{n-1}\right)$ (all congruences are modulo 9 ), we have $2 a_{n-1} \equiv a_{n} \equiv 2008 \equiv 10$, so $a_{n-1} \equiv 5$. But $a_{n-1}<2008$, so $s\left(a_{n-1}\right) \leq 28$ and thus $s\left(a_{n-1}\right)$ can equal 5,14 or 23 . We check $s(2008-5)=s(2003)=5, s(2008-14)=s(1994)=23, s(2008-23)=s(1985)=$ 23. Thus $a_{n-1}$ can equal 1985 or 2003 . As above $2 a_{n-2} \equiv a_{n-1} \equiv 5 \equiv 14$, so $a_{n-2} \equiv 7$. But $a_{n-2}<2003$, so $s\left(a_{n-2}\right) \leq 28$ and thus $s\left(a_{n-2}\right)$ can equal 16 or 25 . Checking as above we see that the only possibility is $s(2003-25)=s(1978)=25$. Thus $a_{n-2}$ can be only 1978. Now $2 a_{n-3} \equiv a_{n-2} \equiv 7 \equiv 16$ and $a_{n-3} \equiv 8$. But $s\left(a_{n-3}\right) \leq 27$ and thus $s\left(a_{n-3}\right)$ can equal 17 or 26 . The check works only for $s(1978-17)=s(1961)=17$. Thus $a_{n-3}=1961$ and similarly $a_{n-4}=1939 \equiv 4, a_{n-5}=1919 \equiv 2$ (if they exist). The search for $a_{n-6}$ requires a residue of 1 . But $a_{n-6}<1919$, so $s\left(a_{n-6}\right) \leq 27$ and thus $s\left(a_{n-6}\right)$ can be equal only to 10 or 19 . The check fails for both $s(1919-10)=s(1909)=19$ and $s(1919-19)=s(1900)=10$. Thus $n \leq 6$ and the case $n=6$ is constructed above (1919, 1939, 1961, 1978, 2003, 2008).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 333
|
NT4 Find all integers $n$ such that $n^{4}+8 n+11$ is a product of two or more consecutive integers.
|
Solution
We will prove that $n^{4}+8 n+11$ is never a multiple of 3 . This is clear if $n$ is a multiple of 3 . If
$n$ is not a multiple of 3 , then $n^{4}+8 n+11=\left(n^{4}-1\right)+12+8 n=(n-1)(n+1)\left(n^{2}+1\right)+12+8 n$, where $8 n$ is the only term not divisible by 3 . Thus $n^{4}+8 n+11$ is never the product of three or more integers.
It remains to discuss the case when $n^{4}+8 n+11=y(y+1)$ for some integer $y$. We write this as $4\left(n^{4}+8 n+11\right)=4 y(y+1)$ or $4 n^{4}+32 n+45=(2 y+1)^{2}$. A check shows that among $n= \pm 1$ and $n=0$ only $n=1$ satisfies the requirement, as $1^{4}+8 \cdot 1+11=20=4 \cdot 5$. Now let $|n| \geq 2$. The identities $4 n^{2}+32 n+45=\left(2 n^{2}-2\right)^{2}+8(n+2)^{2}+9$ and $4 n^{4}+32 n+45=$ $\left(2 n^{2}+8\right)^{2}-32 n(n-1)-19$ indicate that for $|n| \geq 2,2 n^{2}-2<2 y+1<2 n^{2}+8$. But $2 y+1$ is odd, so it can equal $2 n^{2} \pm 1 ; 2 n^{2}+3 ; 2 n^{2}+5$ or $2 n^{2}+7$. We investigate them one by one.
If $4 n^{4}+32 n+45=\left(2 n^{2}-1\right)^{2} \Rightarrow n^{2}+8 n+11=0 \Rightarrow(n+4)^{2}=5$, which is impossible, as 5 is not a perfect square.
If $4 n^{4}+32 n+45=\left(2 n^{2}+1\right)^{2} \Rightarrow n^{2}-8 n-11=0 \Rightarrow(n-4)^{2}=27$ which also fails.
Also $4 n^{4}+32 n+45=\left(2 n^{2}+3\right)^{2} \Rightarrow 3 n^{2}-8 n-9=0 \Rightarrow 9 n^{2}-24 n-27=0 \Rightarrow(3 n-4)^{2}=43$ fails.
If $4 n^{4}+32 n+45=\left(2 n^{2}+5\right)^{2} \Rightarrow 5 n^{2}-8 n=5 \Rightarrow 25 n^{2}-40 n=25 \Rightarrow(5 n-4)^{2}=41$ which also fails.
Finally, if $4 n^{4}+32 n+45=\left(2 n^{2}+7\right)^{2}$, then $28 n^{2}-32 n+4=0 \Rightarrow 4(n-1)(7 n-1)=0$, whence $n=1$ that we already found. Thus the only solution is $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 334
|
NT5 Is it possible to arrange the numbers $1^{1}, 2^{2}, \ldots, 2008^{2008}$ one after the other, in such a way that the obtained number is a perfect square? (Explain your answer.)
|
## Solution
We will use the following lemmas.
Lemma 1. If $x \in \mathbb{N}$, then $x^{2} \equiv 0$ or $1(\bmod 3)$.
Proof: Let $x \in \mathbb{N}$, then $x=3 k, x=3 k+1$ or $x=3 k+2$, hence
$$
\begin{aligned}
& x^{2}=9 k^{2} \equiv 0(\bmod 3) \\
& x^{2}=9 k^{2}+6 k+1 \equiv 1(\bmod 3), \\
& x^{2}=9 k^{2}+12 k+4 \equiv 1(\bmod 3), \text { respectively. }
\end{aligned}
$$
Hence $x^{2} \equiv 0$ or $1(\bmod 3)$, for every positive integer $x$.
Without proof we will give the following lemma.
Lemma 2. If $a$ is a positive integer then $a \equiv S(a)(\bmod 3)$, where $S(a)$ is the sum of the digits of the number $a$.
Further we have
$$
\begin{aligned}
& (6 k+1)^{6 k+1}=\left[(6 k+1)^{k}\right]^{6} \cdot(6 k+1) \equiv 1(\bmod 3) \\
& (6 k+2)^{6 k+2}=\left[(6 k+2)^{3 k+1}\right]^{2} \equiv 1(\bmod 3) \\
& (6 k+3)^{6 k+3} \equiv 0(\bmod 3) \\
& (6 k+4)^{6 k+4}=\left[(6 k+1)^{3 k+2}\right]^{2} \equiv 1(\bmod 3) \\
& (6 k+5)^{6 k+5}=\left[(6 k+5)^{3 k+2}\right]^{2} \cdot(6 k+5) \equiv 2(\bmod 3) \\
& (6 k+6)^{6 k+6} \equiv 0(\bmod 3)
\end{aligned}
$$
for every $k=1,2,3, \ldots$.
Let us separate the numbers $1^{1}, 2^{2}, \ldots, 2008^{2008}$ into the following six classes: $(6 k+1)^{6 k+1}$, $(6 k+2)^{6 k+2},(6 k+3)^{6 k+3},(6 k+4)^{6 k+4},(6 k+5)^{6 k+5},(6 k+6)^{6 k+6}, k=1,2, \ldots$.
For $k=1,2,3, \ldots$ let us denote by
$s_{k}=(6 k+1)^{6 k+1}+(6 k+2)^{6 k+2}+(6 k+3)^{6 k+3}+(6 k+4)^{6 k+4}+(6 k+5)^{6 k+5}+(6 k+6)^{6 k+6}$.
From (3) we have
$$
s_{k} \equiv 1+1+0+1+2+0 \equiv 2(\bmod 3)
$$
for every $k=1,2,3, \ldots$.
Let $A$ be the number obtained by writing one after the other (in some order) the numbers $1^{1}, 2^{2}, \ldots, 2008^{2008}$.
The sum of the digits, $S(A)$, of the number $A$ is equal to the sum of the sums of digits, $S\left(i^{i}\right)$, of the numbers $i^{i}, i=1,2, \ldots, 2008$, and so, from Lemma 2, it follows that
$$
A \equiv S(A)=S\left(1^{1}\right)+S\left(2^{2}\right)+\ldots+S\left(2008^{2008}\right) \equiv 1^{1}+2^{2}+\ldots+2008^{2008}(\bmod 3)
$$
Further on $2008=334 \cdot 6+4$ and if we use (3) and (4) we get
$$
\begin{aligned}
A & \equiv 1^{1}+2^{2}+\ldots+2008^{2008} \\
& \equiv s_{1}+s_{2}+\ldots+s_{334}+2005^{2005}+2006^{2006}+2007^{2007}+2008^{2008}(\bmod 3) \\
& \equiv 334 \cdot 2+1+1+0+1=671 \equiv 2(\bmod 3)
\end{aligned}
$$
Finally, from Lemma 1, it follows that $A$ can not be a perfect square.
|
proof
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 335
|
NT6 Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
|
## Solution
If $n=p$ is prime number, we have
$$
f(p)=f\left(\frac{p}{p}\right)-f(p)=f(1)-f(p)
$$
i.e.
$$
f(p)=\frac{f(1)}{2}
$$
If $n=p q$, where $p$ and $q$ are prime numbers, then
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f(q)-f(p)=\frac{f(1)}{2}-\frac{f(1)}{2}=0
$$
If $n$ is a product of three prime numbers, we have
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=0-f(p)=-f(p)=-\frac{f(1)}{2}
$$
With mathematical induction by a number of prime multipliers we shell prove that: if $n$ is a product of $k$ prime numbers then
$$
f(n)=(2-k) \frac{f(1)}{2}
$$
For $k=1$, clearly the statement (2), holds.
Let statement (2) holds for all integers $n$, where $n$ is a product of $k$ prime numbers.
Now let $n$ be a product of $k+1$ prime numbers. Then we have $n=n_{1} p$, where $n_{1}$ is a product of $k$ prime numbers.
So
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f\left(n_{1}\right)-f(p)=(2-k) \frac{f(1)}{2}-\frac{f(1)}{2}=(2-(k+1)) \frac{f(1)}{2}
$$
So (2) holds for every integer $n>1$.
Now from $f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006$ and because of (2) we have
$$
\begin{aligned}
2006 & =f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right) \\
& =\frac{2-2007}{2} f(1)+\frac{2-2008}{2} f(1)+\frac{2-2009}{2} f(1)=-\frac{3 \cdot 2006}{2} f(1)
\end{aligned}
$$
i.e.
$$
f(1)=-\frac{2}{3}
$$
Since
$$
2007=3^{2} \cdot 223,2008=2^{3} \cdot 251,2009=7^{2} \cdot 41
$$
and because of (2) and (3), we get
$$
\begin{aligned}
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right) & =\frac{2-6}{2} f(1)+\frac{2-12}{2} f(1)+\frac{2-15}{2} f(1) \\
& =-\frac{27}{2} f(1)=-\frac{27}{2} \cdot\left(-\frac{2}{3}\right)=9
\end{aligned}
$$
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 336
|
NT7 Determine the minimal prime number $p>3$ for which no natural number $n$ satisfies
$$
2^{n}+3^{n} \equiv 0(\bmod p)
$$
|
## Solution
We put $A(n)=2^{n}+3^{n}$. From Fermat's little theorem, we have $2^{p-1} \equiv 1(\bmod p)$ and $3^{p-1} \equiv 1(\bmod p)$ from which we conclude $A(n) \equiv 2(\bmod p)$. Therefore, after $p-1$ steps
at most, we will have repetition of the power. It means that in order to determine the minimal prime number $p$ we seek, it is enough to determine a complete set of remainders $S(p)=\{0,1, \ldots, p-1\}$ such that $2^{n}+3^{n} \not \equiv 0(\bmod p)$, for every $n \in S(p)$.
For $p=5$ and $n=1$ we have $A(1) \equiv 0(\bmod 5)$.
For $p=7$ and $n=3$ we have $A(3) \equiv 0(\bmod 7)$.
For $p=11$ and $n=5$ we have $A(5) \equiv 0(\bmod 11)$.
For $p=13$ and $n=2$ we have $A(2) \equiv 0(\bmod 13)$.
For $p=17$ and $n=8$ we have $A(8) \equiv 0(\bmod 17)$.
For $p=19$ we have $A(n) \not \equiv 0(\bmod 19)$, for all $n \in S(19)$.
Hence the minimal value of $p$ is 19 .
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 337
|
NT8 Let $a, b, c, d, e, f$ are nonzero digits such that the natural numbers $\overline{a b c}, \overline{d e f}$ and $\overline{a b c d e f}$ are squares.
a) Prove that $\overline{a b c d e f}$ can be represented in two different ways as a sum of three squares of natural numbers.
b) Give an example of such a number.
|
Solution
a) Let $\overline{a b c}=m^{2}, \overline{d e f}=n^{2}$ and $\overline{a b c d e f}=p^{2}$, where $11 \leq m \leq 31,11 \leq n \leq 31$ are natural numbers. So, $p^{2}=1000 \cdot m^{2}+n^{2}$. But $1000=30^{2}+10^{2}=18^{2}+26^{2}$. We obtain the following relations
$$
\begin{gathered}
p^{2}=\left(30^{2}+10^{2}\right) \cdot m^{2}+n^{2}=\left(18^{2}+26^{2}\right) \cdot m^{2}+n^{2}= \\
=(30 m)^{2}+(10 m)^{2}+n^{2}=(18 m)^{2}+(26 m)^{2}+n^{2}
\end{gathered}
$$
The assertion a) is proved.
b) We write the equality $p^{2}=1000 \cdot m^{2}+n^{2}$ in the equivalent form $(p+n)(p-n)=1000 \cdot m^{2}$, where $349 \leq p \leq 979$. If $1000 \cdot m^{2}=p_{1} \cdot p_{2}$, such that $p+n=p_{1}$ and $p-n=p_{2}$, then $p_{1}$ and $p_{2}$ are even natural numbers with $p_{1}>p_{2} \geq 318$ and $22 \leq p_{1}-p_{2} \leq 62$. For $m=15$ we obtain $p_{1}=500, p_{2}=450$. So, $n=25$ and $p=475$. We have
$$
225625=475^{2}=450^{2}+150^{2}+25^{2}=270^{2}+390^{2}+25^{2}
$$
The problem is solved.
|
225625=475^{2}=450^{2}+150^{2}+25^{2}=270^{2}+390^{2}+25^{2}
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 338
|
NT9 Let $p$ be a prime number. Find all positive integers $a$ and $b$ such that:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}
$$
and
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}
$$
are integers.
|
## Solution
Since $a$ and $b$ are symmetric we can assume that $a \leq b$. Let $d=(a, b), a=d u, b=d v$ and $(u, v)=1$. Then we have:
$$
\frac{a^{2}}{b}+\frac{b^{2}}{a}=\frac{d\left(u^{3}+v^{3}\right)}{u v}
$$
Since,
$$
\left(u^{3}+v^{3}, u\right)=\left(u^{3}+v^{3}, v\right)=1
$$
we deduce that $u \mid d$ and $v \mid d$. But as $(u, v)=1$, it follows that $u v \mid d$.
Now, let $d=u v t$. Furthermore,
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}=\frac{4\left(a^{2}+b^{2}\right)+p(a+b)}{a b}=\frac{4 u v t\left(u^{2}+v^{2}\right)+p(u+v)}{u^{2} v^{2} t}
$$
This implies,
$$
u v \mid p(u+v)
$$
But from our assumption $1=(u, v)=(u, u+v)=(v, u+v)$ we conclude $u v \mid p$. Therefore, we have three cases $\{u=v=1\},\{u=1, v=p\},\{u=p, v=1\}$. We assumed that $a \leq b$, and this implies $u \leq v$.
If $a=b$, we need $\frac{4 a+p}{a}+\frac{4 a+p}{a} \in \mathbb{N}$, i.e. $a \mid 2 p$. Then $a \in\{1,2, p, 2 p\}$. The other condition being fulfilled, we obtain the solutions $(1,1),(2,2),(p, p)$ and $(2 p, 2 p)$.
Now, we have only one case to investigate, $u=1, v=p$. The last equation is transformed into:
$$
\frac{4 a+p}{b}+\frac{4 b+p}{a}=\frac{4 p t\left(1+p^{2}\right)+p(p+1)}{p^{2} t}=\frac{4 t+1+p(1+4 p t)}{p t}
$$
From the last equation we derive
$$
p \mid(4 t+1)
$$
Let $4 t+1=p q$. From here we derive
$$
\frac{4 t+1+p(1+4 p t)}{p t}=\frac{q+1+4 p t}{t}
$$
Now, we have
$$
t \mid(q+1)
$$
or
$$
q+1=\text { st. }
$$
Therefore,
$$
p=\frac{4 t+1}{q}=\frac{4 t+1}{s t-1}
$$
Since $p$ is a prime number, we deduce
$$
\frac{4 t+1}{s t-1} \geq 2
$$
or
$$
s \leq \frac{4 t+3}{2 t}=2+\frac{3}{2 t}<4
$$
Case 1: $s=1, p=\frac{4 t+1}{t-1}=4+\frac{5}{t-1}$. We conclude $t=2$ or $t=6$. But when $t=2$, we have $p=9$, not a prime. When $t=6, p=5, a=30, b=150$.
Case 2: $s=2, p=\frac{4 t+1}{2 t-1}=2+\frac{3}{2 t-1}$. We conclude $t=1, p=5, a=5, b=25$ or $t=2, p=3, a=6, b=18$.
Case 3: $s=3, p=\frac{4 t+1}{3 t-1}$ or $3 p=4+\frac{7}{3 t-1}$. As 7 does not have any divisors of the form $3 t-1$, in this case we have no solutions.
So, the solutions are
$$
(a, b)=\{(1,1),(2,2),(p, p),(2 p, 2 p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)\}
$$
|
(,b)={(1,1),(2,2),(p,p),(2p,2p),(5,25),(6,18),(18,6),(25,5),(30,150),(150,30)}
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 339
|
NT10 Prove that $2^{n}+3^{n}$ is not a perfect cube for any positive integer $n$.
|
## Solution
If $n=1$ then $2^{1}+3^{1}=5$ is not perfect cube.
Perfect cube gives residues $-1,0$ and 1 modulo 9 . If $2^{n}+3^{n}$ is a perfect cube, then $n$ must be divisible with 3 (congruence $2^{n}+3^{n}=x^{3}$ modulo 9 ).
If $n=3 k$ then $2^{3 k}+3^{2 k}>\left(3^{k}\right)^{3}$. Also, $\left(3^{k}+1\right)^{3}=3^{3 k}+3 \cdot 3^{2 k}+3 \cdot 3^{k}+1>3^{3 k}+3^{2 k}=$ $3^{3 k}+9^{k}>3^{3 k}+8^{k}=3^{3 k}+2^{3 k}$. But, $3^{k}$ and $3^{k}+1$ are two consecutive integers so $2^{3 k}+3^{3 k}$ is not a perfect cube.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 340
|
NT11 Determine the greatest number with $n$ digits in the decimal representation which is divisible by 429 and has the sum of all digits less than or equal to 11 .
|
## Solution
Let $A=\overline{a_{n} a_{n-1} \ldots a_{1}}$ and notice that $429=3 \cdot 11 \cdot 13$.
Since the sum of the digits $\sum a_{i} \leq 11$ and $\sum a_{i}$ is divisible by 3 , we get $\sum a_{i}=3,6$ or 9. As 11 divides $A$, we have
$$
11 \mid a_{n}-a_{n-1}+a_{n-2}-a_{n-3}+\ldots
$$
in other words $11 \mid \sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i}$. But
$$
-9 \leq-\sum a_{i} \leq \sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i} \leq \sum a_{i} \leq 9
$$
so $\sum_{i \text { odd }} a_{i}-\sum_{i \text { even }} a_{i}=0$. It follows that $\sum a_{i}$ is even, so $\sum a_{i}=6$ and $\sum_{i \text { odd }} a_{i}=\sum_{i \text { even }} a_{i}=3$.
The number 13 is a divisor of 1001 , hence
$$
13 \mid \overline{a_{3} a_{2} a_{1}}-\overline{a_{6} a_{5} a_{4}}+\overline{a_{9} a_{8} a_{7}}-\overline{a_{12} a_{11} a_{10}}+\ldots
$$
For each $k=1,2,3,4,5,6$, let $s_{k}$ be the sum of the digits $a_{k+6 m}, m \geq 0$; that is
$$
s_{1}=a_{1}+a_{7}+a_{13}+\ldots \text { and so on. }
$$
With this notation, (1) rewrites as
$$
13 \mid 100\left(s_{3}-s_{6}\right)+10\left(s_{2}-s_{5}\right)+\left(s_{1}-s_{4}\right), \text { or } 13 \mid 4\left(s_{6}-s_{3}\right)+3\left(s_{5}-s_{2}\right)+\left(s_{1}-s_{4}\right)
$$
Let $S_{3}=s_{3}-s_{6}, S_{2}=s_{2}-s_{5}$, and $S_{1}=s_{1}-s_{4}$. Recall that $\sum_{i \text { odd }} a_{i}=\sum_{i \text { even }} a_{i}$, which implies $S_{2}=S_{1}+S_{3}$. Then
$$
13\left|4 S_{3}+3 S_{2}-S_{1}=7 S_{3}+2 S_{1} \Rightarrow 13\right| 49 S_{3}+14 S_{1} \Rightarrow 13 \mid S_{1}-3 S_{3}
$$
Observe that $\left|S_{1}\right| \leq s_{1}=\sum_{i \text { odd }} a_{i}=3$ and likewise $\left|S_{2}\right|,\left|S_{3}\right| \leq 3$. Then $-13<S_{1}-3 S_{3}<13$ and consequently $S_{1}=3 S_{3}$. Thus $S_{2}=4 S_{3}$ and $\left|S_{2}\right| \leq 3$ yields $S_{2}=0$ and then $S_{1}=S_{3}=0$. We have $s_{1}=s_{4}, s_{2}=s_{5}, s_{3}=s_{6}$ and $s_{1}+s_{2}+s_{3}=3$, so the greatest number $A$ is $30030000 \ldots$.
|
30030000\ldots
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 341
|
NT12 Solve the equation $\frac{p}{q}-\frac{4}{r+1}=1$ in prime numbers.
|
## Solution
We can rewrite the equation in the form
$$
\begin{gathered}
\frac{p r+p-4 q}{q(r+1)}=1 \Rightarrow p r+p-4 q=q r+q \\
p r-q r=5 q-p \Rightarrow r(p-q)=5 q-p
\end{gathered}
$$
It follows that $p \neq q$ and
$$
\begin{gathered}
r=\frac{5 q-p}{p-q}=\frac{4 q+q-p}{p-q} \\
r=\frac{4 q}{p-q}-1
\end{gathered}
$$
As $p$ is prime, $p-q \neq q, p-q \neq 2 q, p-q \neq 4 q$.
We have $p-q=1$ or $p-q=2$ or $p-q=4$
i) If $p-q=1$ then
$$
q=2, p=3, r=7
$$
ii) If $p-q=2$ then $p=q+2, r=2 q-1$
If $q=1(\bmod 3)$ then $q+2 \equiv 0(\bmod 3)$
$$
q+2=3 \Rightarrow q=1
$$
contradiction.
If $q \equiv-1(\bmod 3)$ then $r \equiv-2-1 \equiv 0(\bmod 3)$
$$
\begin{gathered}
r=3 \\
r=2 q-1=3 \\
q=2 \\
p=4
\end{gathered}
$$
contradiction.
Hence $q=3, p=5, r=5$.
iii) If $p-q=4$ then $p=q+4$.
$r=q-1$
Hence $q=3, p=7, r=2$.
|
(p,q,r)=(3,2,7),
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 342
|
ALG 1. A number $A$ is written with $2 n$ digits, each of whish is 4 , and a number $B$ is written with $n$ digits, each of which is 8 . Prove that for each $n, A+2 B+4$ is a total square.
|
## Solution.
$$
\begin{aligned}
A & =\underbrace{44 \ldots 44}_{2 n}=\underbrace{44 \ldots 4}_{n} \underbrace{44 \ldots 4}_{n}=\underbrace{44 \ldots 4}_{n} \underbrace{400 \ldots 0}_{n}-\underbrace{44 \ldots 4}_{n}+\underbrace{88 \ldots 8}_{n}=\underbrace{44 \ldots 4}_{n} \cdot\left(10^{n}-1\right)+B \\
& =4 \cdot \underbrace{11 \ldots 1}_{n} \cdot \underbrace{99 \ldots 9}_{n}+B=2^{2} \cdot \underbrace{11 \ldots 1}_{n} \cdot 3^{2} \cdot \underbrace{11 \ldots 1}_{n}+B=\underbrace{66}_{n} \ldots 6 \\
& =[\frac{36}{4} \cdot \underbrace{88 \ldots 8}_{n}+B=[3 \cdot \underbrace{22 \ldots 2}_{n}]^{2}+B=\left(\frac{3}{4} B\right)^{2}+B .
\end{aligned}
$$
So,
$$
\begin{aligned}
A+2 B+4 & =\left(\frac{3}{4} B\right)^{2}+B+2 B+4=\left(\frac{3}{4} B\right)^{2}+2 \cdot \frac{3}{4} B \cdot 2+2^{2}=\left(\frac{3}{4} B+2\right)^{2}=(\frac{3}{4} \cdot \underbrace{88 \ldots 8}_{n}+2)^{2} \\
& =(3 \cdot \underbrace{22 \ldots 2}_{n}+2)^{2}=\underbrace{66 \ldots 68^{2}}_{n-1}
\end{aligned}
$$
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 343
|
ALG 2. Let $a, b, c$ be lengths of triangle sides, $p=\frac{a}{b}+\frac{b}{c}+\frac{c}{a}$ and $q=\frac{a}{c}+\frac{c}{b}+\frac{b}{a}$.
Prove that $|p-q|<1$.
|
Solution: One has
$$
\begin{aligned}
a b c|p-q| & =a b c\left|\frac{c-b}{a}+\frac{a-c}{b}+\frac{b-a}{c}\right| \\
& =\left|b c^{2}-b^{2} c+a^{2} c-a c^{2}+a b^{2}-a^{2} b\right|= \\
& =\left|a b c-a c^{2}-a^{2} b+a^{2} c-b^{2} c+b c^{2}+a b^{2}-a b c\right|= \\
& =\left|(b-c)\left(a c-a^{2}-b c+a b\right)\right|= \\
& =|(b-c)(c-a)(a-b)| .
\end{aligned}
$$
Since $|b-c|<a,|c-a|<b$ and $|a-b|<c$ we infere
$$
|(b-c)(c-a)(a-b)|<a b c
$$
and
$$
|p-q|=\frac{|(b-c)(c-a)(a-b)|}{a b c}<1
$$
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 344
|
ALG 3: Let $a, b, c$ be real numbers such that $a^{2}+b^{2}+c^{2}=1$. Prove that. $P=a b+b c+c a-2(a+b+c) \geq-\frac{5}{2}$. Are there values of $a, b, c$, such that $P=-\frac{5}{2}$.
|
Solution: We have $a b+b c+c a=\frac{(a+b+c)^{2}-c^{2}-b^{2}-a^{2}}{2}=\frac{(a+b+c)^{2}-1}{2}$.
If put $t=a+b+c$ we obtain
$$
P=\frac{t^{2}-1}{2}-2 t=\frac{t^{2}-4 t-1}{2}=\frac{(t-2)^{2}-5}{2} \geq-\frac{5}{2}
$$
Obviously $P=-\frac{5}{2}$ when $t=2$, i.e. $a+b+c=2$, or $c=2-a-b$. Substitute in $a^{2}+b^{2}+c^{2}=1$ and obtain $2 a^{2}+2(b-2) a+2 b^{2}-4 b+3=0$. Sinse this quadratic equation has solutions it follows that $(b-2)^{2}-2\left(2 b^{2}-3 b+3\right) \geq 0$, from where
$$
-3 b^{2}+4 b-6 \geq 0
$$
or
$$
3 b^{2}-4 b+6 \leq 0
$$
But $3 b^{2}-4 b+6=3\left(b-\frac{2}{3}\right)^{2}+\frac{14}{3}>0$. The contradiction shows that $P=-\frac{5}{2}$.
Comment: By the Cauchy Schwarz inequality $|t| \leq \sqrt{3}$, so the smallest value of $P$ is attained at $t=\sqrt{3}$ and equals $1-2 \sqrt{3} \approx-2.46$.
|
P\geq-\frac{5}{2}
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 345
|
## ALG 4.
Let $a, b, c$ be rational numbers such that
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{1}{a+b}
$$
Prove that $\sqrt{\frac{c-3}{c+1}}$ is also a rational number
|
Solution. By cancelling the denominators
$$
(a+b)^{2}(1+c)=a b+c\left(a^{2}+b^{2}\right)+a b c^{2}
$$
and
$$
a b(c-1)^{2}=(a+b)^{2}
$$
If $c=-1$, we obtrin the contradiction
$$
\frac{1}{a-b}+\frac{1}{b-a}=\frac{1}{a+b}
$$
Furtherrdore,
$$
\begin{aligned}
(c-3)(c+1) & =(c-1)^{2}-4=\frac{(a+b)^{2}}{a b}-4 \\
& =\frac{(a-b)^{2}}{a b}=\left(\frac{(a-b)(c-1)}{a+b}\right)^{2}
\end{aligned}
$$
Thus
$$
\sqrt{\frac{c-3}{c+1}}=\frac{\sqrt{(c-3)(c+1)}}{c+1}=\frac{|a-b||c-1|}{(c+1)|a+b|} \in \mathrm{Q}
$$
as needed.
|
proof
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 346
|
ALG 5. Let $A B C$ be a scalene triangle with $B C=a, A C=b$ and $A B=c$, where $a_{r} b, c$ are positive integers. Prove that
$$
\left|a b^{2}+b c^{2}+c a^{2}-a^{2} b-b^{2} c-c^{2} a\right| \geq 2
$$
|
Solution. Denote $E=a b^{2}+b c^{2}+c a^{2}-a^{2} b-b^{2} c-c^{2} a$. We have
$$
\begin{aligned}
E= & \left(a b c-c^{2} a\right)+\left(c a^{2}-a^{2} b\right)+\left(b c^{2}-b^{2} c\right)+\left(a b^{2}-a b c\right)= \\
& (b-c)\left(a c-a^{2}-b c+a b\right)=(b-c)\left(a a^{2}-b\right)(c-a)
\end{aligned}
$$
So, $|E|=|a-b| \cdot|b-c| \cdot|c-a|$. By hypothesis each factor from $|E|$ is a positive integer. We shall prove that at least one factor from $|E|$ is greater than 1. Suppose that $|a-b|=|b-c|=|c-a|=1$. It follows that the numbers $a-b, b-c, c-a$ are odd. So, the number $0=(a-b)+(b-c) \div(c-a)$ is olso odd, a contradiction. Hence, $|E| \geq 1 \cdot 1 \cdot 2=2$.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 347
|
ALG 6'. Let $a, b, c$ be positive numbers such that $a b+b c+c a=3$. Prove that
$$
a+b+c \geq a b c+2
$$
|
Solution. Eliminating $c$ gives
$$
a+b+c-a b c=a+b+(1-a b) c=a+b+\frac{(1-a b)(3-a b)}{a+b}
$$
Put $x=\sqrt{a b}$. Then $a+b \geq 2 x$, and since $1<x^{2}<3, \frac{(1-a b)(3-a b)}{a+b} \geq \frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}$.
It then suffices to prove that
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x} \geq 2
$$
This iast inequality follows from the arithrnelic-geomeric means inequadily
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}=\frac{3+x^{4}}{2 x}=\frac{1}{2 x}+\frac{1}{2 x}+\frac{1}{2 x}+\frac{x^{3}}{2} \geq 4\left(\frac{1}{-16}\right)^{\frac{1}{4}}=2
$$
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 349
|
ALG 7 .
Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
|
Solution. We have $y \leq \frac{1+y^{2}}{2}$, hence $\quad$
$$
\frac{1+x^{2}}{1+y+z^{2}} \geq \frac{1+x^{2}}{1+z^{2}+\frac{1+\dot{y}^{2}}{2}}
$$
and the similar inequalities.
Setting $a=1+x^{2}, b=1+y^{2}, c=1+z^{2}$, it sufices to prove that
$$
\frac{a}{2 c+b}+\frac{b}{2 a+c}+\frac{c}{2 b+a} \geq 1
$$
for all $a, b, c \geq 0$.
Put $A=2 c+b, B=2 a+c, C=2 b+a$. Then
$$
a=\frac{C+4 B-2 A}{9}, b=\frac{A+4 C-2 B}{9}, c=\frac{B+4 A-2 C}{9}
$$
and (1) rewrites as
$$
\frac{C+4 B-2 A}{A}+\frac{A+4 C-2 B}{B}+\frac{B+4 A-2 C}{C} \geq 9
$$
and consequently
$$
\frac{C}{A}+\frac{A}{B}+\frac{B}{C}+4\left(\frac{B}{A}+\frac{C}{B}+\frac{A}{C}\right) \geq 15
$$
As $A, B, C>0$, by $A M-G M$ inequality we have
$$
\frac{A}{B}+\frac{B}{C}+\frac{C}{A} \geq 3 \sqrt[3]{\frac{A}{B} \cdot \frac{B}{C} \cdot \frac{C}{A}}
$$
and
$$
\frac{B}{A}+\frac{C}{B}+\frac{A}{C} \geq 3
$$
and we are done.
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 350
|
ALG 8. Prove that there exist two sets $A=\{x, y, z\}$ and $B=\{m, n, p\}$ of positive integers greater than 2003 such that the sets have no common elements and the equalities $x+y+z=m+n+p$ and $x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}$ hold.
|
Solution. Let $A B C$ be a triangle with $B C=a, A C=b, A B=c$ and $ak+3=c
$$
a triangle with such length sides there exist. After the simple calculations we have
$$
\begin{gathered}
A=\left\{3(k+1)^{2}-2,3(k+2)^{2}+4,3(k+3)^{2}-2\right\} \\
B=\left\{3(k+1)^{2}, 3(k+2)^{2}, 3(k+3)^{2}\right\}
\end{gathered}
$$
It easy to prove that
$$
\begin{gathered}
x+y+z=m+n+p=3\left[(k+1)^{2}+(k+2)^{2}+(k+3)^{2}\right] \\
x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}=9\left[(k+1)^{4}+(k+2)^{4}+(k+3)^{4}\right]
\end{gathered}
$$
$>$ From the inequality $3(k+1)^{2}-2>2003$ we obtain $k \geq 25$. For $k=25$ we have an example of two sets
$$
A=\{2026,2191,2350\}, \quad B=\{2028,2187,2352\}
$$
with desired properties.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 351
|
COM 2 Natural numbers 1,2,3, .., 2003 are written in an arbitrary sequence $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$. Let $b_{1}=1 a_{1}, b_{2}=2 a_{2}, b_{3}=3 a_{3}, \ldots, b_{2003}=2003 a_{2003}$, and $B$ be the maximum of the numbers $b_{1}, b_{2}, b_{3}, \ldots, b_{2003}$.
a) If $a_{1}=2003, a_{2}=2002, a_{3}=2001, \ldots, a_{2002}=2, a_{2003}=1$, find the value of $B$.
b) Prove that $B \geq 1002^{2}$.
|
Solution: a) Using the inequality between the arithmetical and geometrical mean, we obtain that $b_{n}=n(2004-n) \leq\left(\frac{n+(2004-n)}{2}\right)^{2}=1002^{2}$ for $n=1,2,3, \ldots, 2003$. The equality holds if and only if $n=2004-n$, i.e. $n=1002$. Therefore, $B=b_{1002}=1002 \times(2004-1002)=1002^{2}$. b) Let $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$ be an arbitrary order of the numbers $1,2,3, \ldots, 2003$. First, we will show that numbers $1002,1003,1004, \ldots, 2003$ cannot occulpy the places numbered $1,2,3$, $\ldots, 1001$ only. Indeed, we have $(2003-1002)+1=1002$ numbers and 1002 places. This means that at least one of the numbers $1002,1003,1004, \ldots, 2003$, say $a_{m}$, lies on a place which number $m$ is greater than 1001 . Therefore, $B \geq m a \geq 1002 \times 1002=1002^{2}$.
|
1002^2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 353
|
COM 3. Prove that amongst any 29 natural numbers there are 15 such that sum of them is divisible by 15 .
|
Solution: Amongst any 5 natural numbers there are 3 such that sum of them is divisible by 3 . Amongst any 29 natural numbers we can choose 9 groups with 3 numbers such that sum of numbers in every group is divisible by 3. In that way we get 9 natural numbers such that all of them are divisiblc by 3. It is easy to see that amongst any 9 natural numbers there are 5 such that sum of them is divisible by 5 . Since we have 9 numbers, all of them are divisible by 3 , there are 5 such that sum of them is divisible by 15 .
## $\operatorname{COM} 4$.
$n$ points are given in a plane, not three of them colinear. One observes that no matter how we label the points from 1 to $n$, the broken line joining the points $1,2,3, \ldots, n$ (in this order) do not intersect itself.
Find the maximal value of $n$.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 354
|
COM 5. If $m$ is a number from the set $\{1,2,3,4\}$ and each point of the plane is painted in red or blue, prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$.
|
Solution. Suppose that in the plane there no exists an equilateral triangle with the vertices of the same colour and length side $m=1,2,3,4$.
First assertion: we shall prove that in the plane there no exists a segment with the length 2 such that the ends and the midpint of this segment have the same colour. Suppose that the segment $X Y$ with length 2 have the midpoint $T$ such that the points $X, Y, T$ have the same colour (for example, red). We construct the equilateral triangle. $X Y Z$. Hence, the point $Z$ is blue. Let $U$ and $V$ be the midpoints of the segments $X Z$ and $Y Z$ respectively. So, the points $U$ and $V$ are blue. We obtain a contradiction, because the equilateral triangle $U V Z$ have three blue vertices.
Second assertion: in the same way we prove that in the plane there no exists a segment with the length 4 such that the ends and the midpoint of this segment have the same colour.
Consider the equilateral triangle $A B C$ with length side 4 and divide it into 16 equilateral triangles with length sides 1. L $0: D$ be the midpoint of the segment $A B$. The vertices $A, B, C$ don't have the same colour. WLOG we suppose that $A$ and $B$ are red and $C$ is blue. So, the point $D$ is blue too. We shall investigate the following cases:
a) The midpoints $E$ and $F$ of the sides $A C$ and, respectively, $B C$ are red. From the first assertion it follows that the midpoints $M$ and $N$ of the segments $A E$ and, respectively, $B F$ are blue. Hence, the equilateral triangle $M N C$ have three blue vertices, a contradiction.
b) Let $E$ is red and $F$ is blue. The second one position of $E$ and $F$ is simmetrical. If $P, K, L$ are the midpoints of the segments $C F, A D, B D$ respectively, then by first assertion $P$ is red, $M$ is blue and $N$ is red. This imply that $K$ and $L$ are blue. So, the segment $K L$ with length 2 has the blue ends and blue midpoint, a contradiction.
c) If $E$ and $F$ are blue, then the equilateral triangle $E F C$ has three blue vertices, a contradiction.
Hence, in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m \in\{1,2,3,4\}$.
Comment: The formuation of the problem suggests that one has to find 4 triangles, one for each $m$ from the set $\{1,2,3,4\}$ whereas the solution is for one $m$. A better formulation is:
Each point of the plane is painted in red or blue. Prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m$ is some number from the set $\{1,2,3,4\}$.
|
proof
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 355
|
GEO 1. Is there a convex quadrilateral, whose diagonals divide it into four triangles, such that their areas are four distinct prime integers.
|
Solution. No. Let the areas of those triangles be the prime numbers $p, q, r$ and $t$. But for the areas of the triangles we have $\mathrm{pq}=\mathrm{rt}$, where the triangles with areas $\mathrm{p}$ and $\mathrm{q}$ have only a common vertex. This is not possible for distinct primes.
|
proof
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 356
|
GEO 2. Is there a triangle whose area is $12 \mathrm{~cm}^{2}$ and whose perimeter is $12 \mathrm{~cm}$.
|
Solution. No. Let $\mathrm{r}$ be the radius of the inscribed circle. Then $12=6 \mathrm{r}$, i.e. $\mathrm{r}=2 \mathrm{~cm}$. But the area of the inscribed circle is $4 \pi>12$, and it is known that the area of any triangle is bigger than the area of its inscribed circle.
|
proof
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 357
|
## GEO 3.
Let $G$ be the centroid of the the triangle $A B C$. Reflect point $A$ across $C$ at $A^{\prime}$. Prove that $G, B, C, A^{\prime}$ are on the same circle if and only if $G A$ is perpendicular to $G C$.
|
Solution. Observe first that $G A \perp G C$ if and only if $5 A C^{2}=A B^{2}+B C^{2}$. Indeed,
$$
G A \perp G C \Leftrightarrow \frac{4}{9} m_{a}^{2}+\frac{4}{9} m_{c}^{2}=b^{2} \Leftrightarrow 5 b^{2}=a^{2}+c^{2}
$$
Moreover,
$$
G B^{2}=\frac{4}{9} m_{b}^{2}=\frac{2 a^{2}+2 c^{2}-b^{2}}{9}=\frac{9 b^{2}}{9}=b^{2}
$$
hence $G B=A C=C A^{\prime}$ (1). Let $C^{\prime}$ be the intersection point of the lines $G C$ and $A B$. Then $C C^{\prime}$ is the middle line of the triangle $A B A^{\prime}$, hence $G C \| B A^{\prime}$. Consequently, $G C A^{\prime} B$ is a trapezoid. From (1) we find that $G C A^{\prime} B$ is isosceles, thus cyclic, as needed.
Conversely, since $G C A^{\prime} B$ is a cyclic trapezoid, then it is also isosceles. Thus $C A^{\prime}=$ $G B$, which leads to (1).
Comment: An alternate proof is as follows:
Let $M$ be the midpoint of $A C$. Then the triangles $M C G$ and $M A^{\prime} B$ are similar. So $G C$ is parallel to $A^{\prime} B$.
$G A \perp G C$ if and only if $G M=M C$. By the above similarity, this happen if and only if $A^{\prime} C=G B$; if and only if the trapezoid is cyclic.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 358
|
GEO 5. Let three congruent circles intersect in one point $M$ and $A_{1}, A_{2}$ and $A_{3}$ be the other intersection points for those circles. Prove that $M$ is a.orthocenter for a triangle $A_{1} A_{2} A_{3}$.
|
Solution: The quadrilaterals $\mathrm{O}_{3} M O_{2} A_{1}, \mathrm{O}_{3} M O_{1} A_{2}$ and $O_{1} M O_{2} A_{3}$ are rombes. Therefore, $O_{2} A_{1} \| M O_{3}$ and $M O_{3} \| O_{1} A_{2}$, which imply $O_{2} A_{1} \| O_{1} A_{2}$. Because $O_{2} A_{1}=O_{3}{ }^{*} M=O_{1} A_{2}$ the quadrilateral $O_{2} A_{1} A_{2} O_{1}$ is parallelogram and then $A_{1} A_{2} \| O_{1} O_{2}$ and $A_{1} A_{2}=O_{1} O_{2}$. Similary, $A_{2} A_{3} \| O_{2} O_{3}$ and $A_{2} A_{3}=O_{2} O_{3} ; A_{3} A_{1} \| O_{3} O_{1}$ and $A_{3} A_{1}=O_{3} O_{1}$. The triangles $A_{1} A_{2} A_{3}$ and $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are congruent.
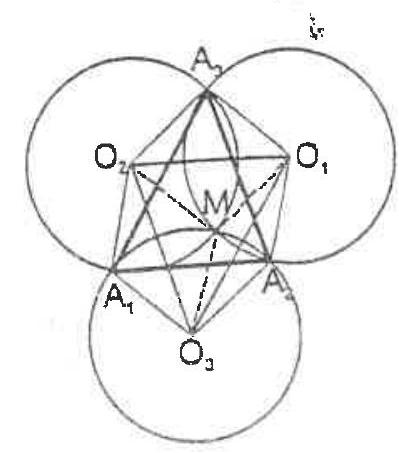
Since $A_{3} M \perp O_{1} O_{2}$ and $O_{1} O_{2} \| A_{1} A_{2}$ we infere $A_{3} M \perp A_{1} A_{2}$. Similary, $A_{2} M \perp A_{1} A_{3}$ and $A_{1} M \perp A_{2} A_{3}$. Thus, $M$ is the orthocenter for the triangle $A_{1} A_{2} A_{3}$.
## GEO.6.
Consider an isosceles triangle $A B C$ with $A B=A C$. A semicircle of diameter $E F$, lying on the side $B C$, is tangent to the lines $A B$ and $A C$ at $M$ and $N$, respectively. The line $A E$ intersects again the semicircle at point $P$.
Prove that the line PF passes through the midpoint of the chord $M N$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 359
|
GEO 7. Through a interior point of a triangle, three lines parallel to the sides of the triangle are constructed. In that way the triangle is divided on six figures, areas equal $a, b, c, \alpha, \beta, \gamma$ (see the picture).
Prove that
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant \frac{3}{2}
$$
|
Solution: We will prove the inequality in two steps. First one is the following
Lemma: Let $A B C$ be a triangle, $E$ arbitrary point on the side $A C$. Parallel lines to $A B$ and $B C$, drown through $E$ meet sides $B C$ and $A B$ in points $F$. and $D$ respectively. Then: $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$ ( $P_{X}$ is area for the figure $X)$.
The triangles $A D E$ and $E F C$ are similar. Then:
$$
\frac{P_{B D E F}}{2 P_{A D E}}=\frac{P_{B D E}}{P_{A D E}}=\frac{B D}{A D}=\frac{E F}{A D}=\frac{\sqrt{P_{E F C}}}{\sqrt{P_{A D E}}}
$$
Hence, $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$.
Using this lemma one has $\alpha=2 \sqrt{b c}, \beta=2 \sqrt{a c}, \gamma=2 \sqrt{a b}$. The GML-AM mean inequality provides
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant 3 \sqrt[3]{\frac{a b c}{\alpha \beta \gamma}}=3 \sqrt[3]{\frac{a b c}{2^{3} \sqrt{a^{2} b^{2} c^{2}}}}=\frac{3}{2}
$$
BULGARIA
| Leader: | Chavdar Lozanov |
| :--- | :--- |
| Deputy Leader: | Ivan Tonov |
| Contestants: | Asparuh Vladislavov Hriston |
| | Tzvetelina Kirilova Tzeneva |
| | Vladislav Vladilenon Petkov |
| | Alexander Sotirov Bikov |
| | Deyan Stanislavov Simeonov |
| | Anton Sotirov Bikov |
## CYPRUS
| Leader: | Efthyvoulos Liasides |
| :--- | :--- |
| Deputy Leader: | Andreas Savvides |
| Contestants: | Marina Kouyiali |
| | Yiannis loannides |
| | Anastasia Solea |
| | Nansia Drakou |
| | Michalis Rossides |
| | Domna Fanidou |
| Observer: | Myrianthi Savvidou |
FORMER YUGOSLAV
REPUBLIC of MACEDONIA
| Leader: | Slavica Grkovska |
| :--- | :--- |
| Deputy Leader: | Misko Mitkovski |
| Contestants: | Aleksandar lliovski |
| | Viktor Simjanovski |
| | Maja Tasevska |
| | Tanja Velkova |
| | Matej Dobrevski |
| | Oliver Metodijev |
## GREECE
Leader: Anargyros Felouris
Deputy Leader: Ageliki Vlachou
Contestants: Theodosios Douvropoulos
Marina lliopoulou
Faethontas Karagiannopoulos
Stefanos Kasselakis
Fragiskos Koufogiannis
Efrosyni Sarla
ROMANIA
| Leader: | Dan Branzei |
| :--- | :--- |
| Deputy Leader: | Dinu Serbanescu |
| Contestants: | Dragos Michnea |
| | Adrian Zahariuc |
| | Cristian Talau |
| | Beniämin Bogosel |
| | Sebastian Dumitrescu |
| | Lucian Turea |
## TURKEY
Leader:
Halil Ibrahim Karakaş
\&Deputy Leader: Duru Türkoğlu
Contestants: Sait Tunç
Anmet Kabakulak
Türkü Çobanoğlu
Burak Sağlam
Ibrahim Çimentepe
Hale Nur Kazaçeşme
## YUGOSLAVIA
(SERBIA and MONTENEGRO)
| Leader: | Branislav Popovic |
| :--- | :--- |
| Deputy Leader: | Marija Stanic |
| Contestants: | Radojevic Mladen |
| | Jevremovic Marko |
| | Djoric Milos |
| | Lukic Dragan |
| | Andric Jelena |
| | Pajovic Jelena |
## TURKEY-B
## Leader:
Deputy Leader: Contestants:
Ahmet Karahan
Deniz Ahçihoca ..... Havva Yeşildağl|
Çağıl Şentip
Buse Uslu
Ali Yilmaz
Demirhan Çetereisi
Yakup Yildirim
## REPUBLIC of MOLDOVA
| Leader: | Ion Goian |
| :--- | :--- |
| Deputy Leader: | Ana Costas |
| Contestants: | lurie Boreico |
| | Andrei Frimu |
| | Mihaela Rusu |
| | Vladimir Vanovschi |
| | Da Vier: |
| | Alexandru Zamorzaev |
1.Prove that $7^{n}-1$ is not divisible by $6^{n}-1$ for any positive integer $n$.
2. 2003 denars were divided in several bags and the bags were placed in several pockets. The number of bags is greater than the number of denars in each pocket. Is it true that the number of pockets is greater than the number of denars in one of the bags?
3. In the triangle $\mathrm{ABC}, R$ and $r$ are the radii of the circumcircle and the incircle, respectively; $a$ is the longest side and $h$ is the shortest altitude. Prove that $R / r>a / h$.
4. Prove that for all positive numbers $x, y, z$ such that $x+y+z=1$ the following inequality holds
$$
\frac{x^{2}}{1+y}+\frac{y^{2}}{1+z}+\frac{z^{2}}{1+x} \leq 1
$$
5.Is it possible to cover a $2003 \times 2003$ board with $1 \times 2$ dominoes placed horizontally and $1 \times 3$ threeminoes placed vertically?
## THE 47-th MATHEMATIAL OLYMPIAD OF REPUBLIC OF MOLDOVA Chişinău, March 9-12, 2003
7.1 Let $m>n$ be pozitive integers. For every positive integers $k$ we define the number $a_{k}=(\sqrt{5}+2)^{k}+$ $(\sqrt{5}-2)^{k}$. Show that $a_{m+n}+a_{m-n}=a_{m} \cdot a_{n}$.
T. Fild all five digits numbers $\overline{a b c d e}$, written in decimal system, if it is known that $\overline{a b} c d e-\overline{e b c d a}=69993$, $\overline{b c d}-\overline{d c b}=792, \overline{b c}-\overline{c b}=72$.
7.3 In the triangle $A B C$ with semiperemeter $p$ the points $M, N$ and $P$ lie on the sides $(B C),(C A)$ and - (AB) respectively. Show that $pb \geq$ 10. Prove that this equation has two irrational solutions. (The number $m$ is triangular, if $m=n(n-1) / 2$ for certain positive integer $n \geq 1$ ).
9.3 The distinct points $M$ and $N$ lie on the hypotenuse ( $A C)$ of the right isosceles triangle $A B C$ so that $M \in(A N)$ and $M N^{2}=A M^{2}+C N^{2}$. Prove that $m(\angle M B N)=45^{\circ}$.
9.4 Find all the functions $f: N^{*} \rightarrow N^{*}$ which verify the relation $f(2 x+3 y)=2 f(x)+3 f(y)+4$ for every positive integers $x, y \geq 1$.
9.5 The numbers $a_{1}, a_{2}, \ldots, a_{n}$ are the first $n$ positive integers with the property that the number $8 a_{k}+1$ is a perfect square for every $k=1,2, \ldots, n$. Find the sum $S_{n}=a_{1}+a_{2}+\ldots+a_{n}$.
9.6 Find all real solutions of the equation $x^{4}+7 x^{3}+6 x^{2}+5 \sqrt{2003} x-2003=0$.
9.7 The side lengths of the triangle $A B C$ satisfy the relations $a>b \geq 2 c$. Prove that the altitudes of the triangle $A B C$ can not be the sides of any triangle.
9.8 The base of a pyramid is a convex polygon with 9 sides. All the lateral edges of the pyramid and all the liagunads ui the base are coloured in a random way in red or blue. Pröve that there exist at least three vertices of the pyramid which belong to a triangle with the sides coloured in the same colour.
10.1 Find all prime numbers $a, b$ and $c$ for which the equality $(a-2)!+2 b!=22 c-1$ holds.
10.2 Solve the system $x+y+z+t=6, \sqrt{1-x^{2}}+\sqrt{4-y^{2}}+\sqrt{9-z^{2}}+\sqrt{16-t^{2}}=8$.
10.3 In the scalen triangle $A B C$ the points $A_{1}$ and $B_{1}$ are the bissectrices feets, drawing from the vertices $A$ and $B$ respectively. The straight line $A_{1} B_{1}$ intersect the line $A B$ at the point $D$. Prove that one of the angles $\angle A C D$ or $\angle B C D$ is obtuze and $m(\angle A C D)+m(\angle B C D)=180^{\circ}$.
10.4 Let $a>1$ be not integer number and $a \neq \sqrt[2]{q}$ for every positive integers $p \geq 2$ and $q \geq 1$, $k=\left[\log _{a} n\right] \geq 1$, where $[x]$ is the integral part of the real number $x$. Prove that for every positive integer $n \geq 1$ the equality
$$
\left[\log _{a} 2\right]+\left[\log _{a} 3\right]+\ldots+\left[\log _{a} n\right]+[a]+\left[a^{2}\right]+\ldots+\left[a^{k}\right]=n k
$$
holds.
10.5 The rational numbers $p, q, r$ satisfy the relation $p q+p r+q r=1$. Prove that the number $\left(1+p^{2}\right)\left(1+q^{3}\right)\left(1+r^{2}\right)$ is a square of any rational number.
10.6 Let $n \geq 1$ be a positive integer. For every $k=1,2, \ldots, n$ the functions $f_{k}: R \rightarrow R, f_{k}(x)=$ $a_{k} x^{2}+b_{k} x+c_{k}$ with $a_{k} \neq 0$ are given. Find the greatest possible number of parts of the rectangular plane $x O y$ which can be obtained by the intersection of the graphs of the functions $f_{k}(k=1,2, \ldots, n)$.
10.7 The circle with the center $O$ is tangent to the sides $[A B],[B C],[C D]$ and $[D A]$ of the convex quadrilateral $A B C D$ at the points $M, N, \mathcal{K}$ and $L$ respectively. The straight lines $M N$ and $A C$ are parallel and the straight line $M K$ intersect the line $L N$ at the point $P$. Prove that the points $A, M, P, O$ and $L$ are concyclic.
10.8 Find all integers $n$ for which the number $\log _{2 n-1}\left(n^{2}+2\right)$ is rational.
11.1 Let $a, b, c, d \geq 1$ be arbitrary positive numbers. Prove that the equations system $a x-y z=$ $c, \quad b x-y t=-d$. has at least a solution $(x, y, z, t)$ in positive integers.
11.2 The sequences $\left(a_{n}\right)_{n \geq 0}$ and $\left(b_{n}\right)_{n \geq 0}$ satisfy the conditions $(1+\sqrt{3})^{2 n+1}=a_{n}+b_{n} \sqrt{3}$ and $a_{n}, b_{n} \in Z$. Find the recurrent relation for each of the sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$.
11.3 The triangle $A B C$ is rightangled in $A, A C=b, A B=c$ and $B C=a$. The halfstraight line ( $A z$ is perpendicular to the plane $(A B C), M \in(A z$ so that $\alpha, \beta, \gamma$ are the mesures of the angles, formed by the edges $M B, M C$ and the plane ( $M B C$ ) with the plane ( $A B C$ ) respectively. In the set of the triangular pyramids MABC on consider the pyramids with the volumes $V_{1}$ and $V_{2}$ which satisfy the relations $\alpha+\beta+\gamma=\pi$ and $\alpha+\beta+\gamma=\pi / 2$ respectively. Prove the equality $\left(V_{1} / V_{2}\right)^{2}=(a+b+c)(1 / a+1 / b+1 / c)$.
11.4 Find all the functions $f:[0 ;+\infty) \rightarrow[0 ;+\infty)$ which satisfy the conditions: : $f(x f(y)) \cdot f(y)=$ $f(x+y)$ for every $x, y \in[0 ;+\infty) ; f(2)=0 ; f(x) \neq 0$ for every $x \in[0 ; 2)$.
11.5 Let $02 R \sin \alpha$.
12.4 The real numbers $\alpha, \beta, \gamma$ satisfy the relations $\sin \alpha+\sin \beta+\sin \gamma=0$ and $\cos \alpha+\cos \beta+\cos \gamma=0$. Find all positive integers $n \geq 0$ for-which $\sin (n \alpha+\pi / 4)+\sin (n \beta+\pi / 4)+\sin (n \gamma+\pi / 4)=0$.
12.5 For every positive integer $n \geq 1$ we define the polynomial $P(X)=X^{2 n}-X^{2 n-1}+\ldots-X+1$, Find the remainder of the division of the polynomial $P\left(X^{2 n+1}\right)$ by the polynomial $P(X)$.
12.6 Fie $n \in N$. Find all the primitives of the function
$$
f: R \rightarrow R, \quad f(x)=\frac{x^{3}-9 x^{2}+29 x-33}{\left(x^{2}-6 x+10\right)^{n}}
$$
12.7 In a rectangular system $x O y$ the graph of the function $f: R \rightarrow R, f(x)=x^{2}$ is drawn. The ordered triple $B, A, C$ has distinct points on the parabola, the point $D \in(B C)$ such that the straight line $A D$ is parallel to the axis $O y$ and the triangles $B A D$ and $C A D$ have the areas $s_{1}$ and $s_{2}$ respectively. Find the length of the segment $[A D]$.
12.8 Let $\left(F_{n}\right)_{n \in N^{*}}$ be the Fibonacci sequence so that: $F_{1}=1, F_{2}=1, F_{n+1}=F_{n}+F_{n-1}$ for every positive integer $n \geq 2$. Shown that $F_{n}<3^{n / 2}$ and calculate the limit $\lim _{n \rightarrow \infty}\left(F_{1} / 2+F_{2} / 2^{2}+\ldots+F_{n} / 2^{n}\right)$.
## The first selection test for IMO 2003 and BMO 2003, March 12, 2003
B1. Each side of the arbitrary triangle is divided into 2002 congruent segments. After that each interior division point of the side is joined with opposite vertex. Prove that the number of obtained regions of the triangle is divisible by 6 .
B2. The positive real numbers $x, y$ and $z$ satisfy the relation $x+y+z \geq 1$. Prove the inequality
$$
\frac{x \sqrt{x}}{y+z}+\frac{y \sqrt{y}}{x+z}+\frac{z \sqrt{z}}{x+y} \geq \frac{\sqrt{3}}{2}
$$
B3. The quadrilateral $A B C D$ is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the diagonals $[A C]$ and $[B D]$ respectively and $P$ is the intersection point of the diagonals. It is known that the points $O, M, N$ si $P$ are distinct. Prove that the points $O, M, B$ and $D$ are concyclic if and only if the points $O, N, A$ and $C$ are concyclic.
B4. Prove that the equation $1 / a+1 / b+1 / c+1 /(a b c) \doteq 12 /(a+b+c)$ has many solutions $(a, b, c)$ in strictly positive integers.
## The second selection test for IMO 2003, March 22, 2003
B5. Let $n \geq 1$ be positive integer. Find all polynomials of degree $2 n$ with real coefficients
$$
P(X)=X^{2 n}+(2 n-10) X^{2 n-1}+a_{2} X^{2 n-2}+\ldots+a_{2 n-2} X^{2}+(2 n-10) X+1
$$
-if it is known that they have positive real roots.
B6. The triangle $A B C$ has the semiperimeter $p$, the circumradius $R$, the inradius $r$ and $l_{a,}, l_{b}, l_{c}$ are the lengths of internal bissecticies, drawing from the vertices $A, B$ and $C$ respectively. Prove the inequality $l_{a} l_{b}+l_{b} l_{c}+l_{c} l_{a} \leq p \sqrt{3 r^{2}+12 R r}$.
B7. The points $M$ and $N$ are the tangent points of the sides $[A B]$ and $[A C]$ of the triangle $A B C$ to the incircle with the center $I$. The internal bissectrices, drawn from the vertices $B$ and $C$, intersect the straight line $M N$ at points $P$ and $Q$ respectively. If $F$ is the intersection point of the swtraight lines $C P$ and $B Q$, then prove that the straight lines $F I$ and $B C$ are perpendicular.
B8. Let $n \geq 4$ be the positive integer. On the checkmate table with dimensions $n \times n$ we put the coins. One consider the diagonal of the table each diagonal with at least two unit squares. What is the smallest number of coins put on the table so that on the each horizontal, each vertical and each diagonal there exists att least one coin. Prove the answer.
## The third selection test for IMO 2003, March 23, 2003
B9. Let $n \geq 1$ be positive integer. A permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the numbers $(1,2, \ldots, n)$ is called quadratique if among the numbers $a_{1}, a_{1}+a_{2}, \ldots, a_{1}+a_{2}+\ldots+a_{n}$ there exist at least a perfect square. Find the greatest number $n$, which is less than 2003 , such that every permutation of the numbers $(1,2, \ldots, n)$ will be quadratique.
B10. The real numbers $a_{1}, a_{2}, \ldots, a_{2003}$ satisfy simultaneousiy the relations: $a_{i} \geq 0$ for all $i=$ $1,2, \ldots, 2003 ; \quad a_{1}+a_{2}+\ldots+a_{2003}=2 ; \quad a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2003} a_{1}=1$. Find the smallest value of the sum $a_{1}^{2}+a_{2}^{2}+\ldots+a_{2003}^{2}$.
B11. The arbitrary point $M$ on the plane of the triangle $A B C$ does not belong on the straight lines $A B, B C$ and $A C$. If $S_{1}, S_{2}$ and $S_{3}$ are the areas of the triangles $A M B, B M C$ and $A M C$ respectively, find the geometrical locus of the points $M$ which satisfy the relation $\left(M A^{2}+M B^{2}+M C^{2}\right)^{2}=16\left(S_{1}^{2}+S_{2}^{2}+S_{3}^{2}\right)$.
812. Let $n \geq 1$ be a positive integer. A square table of dimensions $n \times n$ is full arbitrarly completed $\because$ the numb so, shat every number appear exactly conce the table. from cack fine one select the smallest number and the greatest of them is denote by $x$. From each column one select the greatest number and the smallest of them is denote by $y$. The table is called equilibrated if $x=y$. How match equilibrated tables there exist?
## The first selection test for JBMO 2003, April 12, 2003
JB1. Let $n \geq 2003$ be a positive integer such that the number $1+2003 n$ is a perfect square. Prove that the number $n+1$ is equal to the sum of 2003 positive perfect squares.
JB2. The positive real numbers $a, b, c$ satisfy the relation $a^{2}+b^{2}+c^{2}=3 a b c$. Prove the inequality
$$
\frac{a}{b^{2} c^{2}}+\frac{b}{c^{2} a^{2}}+\frac{c}{a^{2} b^{2}} \geq \frac{9}{a+b+c}
$$
JB3. The quadrilateral $A B C D$ with perpendicular diagonals is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the sides $[B C]$ and $[C D]$ respectively. Find the value of the ratio of areas of the figures $O M C N$ and $A B C D$.
JB4. Let $m$ and $n$ be the arbitrary digits of the decimal system and $a, b, c$ be the positive distinct integers of the form $2^{m} \cdot 5^{n}$. Find the number of the equations $a x^{2}-2 b x+c=0$, if it is known that each equation has a single real solution.
## The second selection test for JMBO 2003, April 13, 2003
JB5. Prove that each positive integer is equal to a difference of two positive integers with the same number of the prime divisors.
JB6. The real numbers $x$ and $y$ satisfy the equalities
$$
\sqrt{3 x}\left(1+\frac{1}{x+y}\right)=2, \quad \sqrt{7 y}\left(1-\frac{1}{x+y}\right)=4 \sqrt{2}
$$
Find the numerical value of the ratio $y / x$.
$J B 7$. The triangle $A B C$ is isosceles with $A B=B C$. The point $F$ on the side $[B C]$ and the point $D$ on the side $[A C]$ are the feets of the internal bissectrix drawn from $A$ and altitude drawn from $B$ respectively so that $A F=2 B D$. Find the measure of the angle $A B C$.
JB8. In the rectangular coordinate system every point with integer coordinates is called laticeal point. Let $P_{n}(n, n+5)$ be a laticeal point and denote by $f(n)$ the number of laticeal points on the open segment $\left(O P_{n}\right)$, where the point $O(0,0)$ is the coordinates system origine. Calculate the number $f(1)+f(2)+$ $f(3)+\ldots+f(2002)+f(2003)$.
7 th Junior Balkan Mathematical O-lympiad
$20-25$ Jun e, 20.03 I $\mathrm{m}$ i r $\quad$. $\quad$ u rke y
## English Version
1. Let $n$ be a positive integer. A number $A$ consists of $2 n$ digits, each of which is 4 ; and a number $B$ consists of $n$ digits, each of which is 8 . Prove that $A+2 B+4$ is a perfect square.
\&
2. Suppose there are $n$ points in a plane no three of which are collinear with the following property:
If we label these points as $A_{1}, A_{2}, \ldots, A_{n}$ in any way whatsoever, the broken line $A_{1} A_{2} \ldots A_{n}$ does not intersect itself.
Find the maximal value that $n$ can have.
3. Let $k$ be the circumcircle of the triangle $A B C$. Consider the arcs $\overparen{A B}, \widehat{B C}, \widetilde{C A}$ such that $C \notin \widetilde{A B}, A \notin \widetilde{B C}, B \notin \widetilde{C A}$. Let $D, E$ and $F$ be the midpoints of the arcs $\widehat{B C}, \overparen{C A}, \overparen{A B}$, respectively. Let $G$ and $H$ be the points of intersection of $D E$ with $C B$ and $C A$; let $I$ and $J$ be the points of intersection of $D F$ with $B C$ and $B A$, respectively. Denote the midpoints of $G H$ and $I J$ by $M$ and $N$, respectively.
a) Find the angles of the triangle $D M N$ in terms of the angles of the triangle $A B C$.
b) If $O$ is the circumcentre of the triangle $D M N$ and $P$ is the intersection point of $A D$ and $E F$, prove that $O, P, M$ and $N$ lie on the same circle.
4. Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
## Romanian Version
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 360
|
87.1. Nine journalists from different countries attend a press conference. None of these speaks more than three languages, and each pair of the journalists share a common language. Show that there are at least five journalists sharing a common language.
|
Solution. Assume the journalists are $J_{1}, J_{2}, \ldots, J_{9}$. Assume that no five of them have a common language. Assume the languages $J_{1}$ speaks are $L_{1}, L_{2}$, and $L_{3}$. Group $J_{2}, J_{3}$, $\ldots, J_{9}$ according to the language they speak with $J_{1}$. No group can have more than three members. So either there are three groups of three members each, or two groups with three members and one with two. Consider the first alternative. We may assume that $J_{1}$ speaks $L_{1}$ with $J_{2}, J_{3}$, and $J_{4}, L_{2}$ with $J_{5}, J_{6}$, and $J_{7}$, and $L_{3}$ with $J_{8}, J_{9}$, and $J_{2}$. Now $J_{2}$ speaks $L_{1}$ with $J_{1}, J_{3}$, and $J_{4}, L_{3}$ with $J_{1}, J_{8}$, and $J_{9}$. $J_{2}$ must speak a fourth language, $L_{4}$, with $J_{5}, J_{6}$, and $J_{7}$. But now $J_{5}$ speaks both $L_{2}$ and $L_{4}$ with $J_{2}, J_{6}$, and $J_{7}$. So $J_{5}$ has to use his third language with $J_{1}, J_{4}, J_{8}$, and $J_{9}$. This contradicts the assumption we made. So we now may assume that $J_{1}$ speaks $L_{3}$ only with $J_{8}$ and $J_{9}$. As $J_{1}$ is not special, we conclude that for each journalist $J_{k}$, the remaining eight are divided into three mutually exclusive language groups, one of which has only two members. Now $J_{2}$ uses $L_{1}$ with three others, and there has to be another language he also speaks with three others. If this were $L_{2}$ or $L_{3}$, a group of five would arise (including $J_{1}$ ). So $J_{2}$ speaks $L_{4}$ with three among $J_{5}, \ldots, J_{9}$. Either two of these three are among $J_{5}, J_{6}$, and $J_{7}$, or among $J_{8}, J_{9}$. Both alternatives lead to a contradiction to the already proved fact that no pair of journalists speaks two languages together. The proof is complete.
Figure 1.
|
proof
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 362
|
87.2. Let $A B C D$ be a parallelogram in the plane. We draw two circles of radius $R$, one through the points $A$ and $B$, the other through $B$ and $C$. Let $E$ be the other point of
intersection of the circles. We assume that $E$ is not a vertex of the parallelogram. Show that the circle passing through $A, D$, and $E$ also has radius $R$.
|
Solution. (See Figure 1.) Let $F$ and $G$ be the centers of the two circles of radius $R$ passing through $A$ and $B$; and $B$ and $C$, respectively. Let $O$ be the point for which the the rectangle $A B G O$ is a parallelogram. Then $\angle O A D=\angle G B C$, and the triangles $O A D$ and $G B C$ are congruent (sas). Since $G B=G C=R$, we have $O A=O D=R$. The quadrangle $E F B G$ is a rhombus. So $E F\|G B\| O A$. Moreover, $E F=O A=R$, which means that $A F E O$ is a parallelogram. But this implies $O E=A F=R$. So $A, D$, and $E$ all are on the circle of radius $R$ centered at $O$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 363
|
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
Solution. Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 364
|
87.4. Let $a, b$, and $c$ be positive real numbers. Prove:
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
|
Solution. The arithmetic-geometric inequality yields
$$
3=3 \sqrt[3]{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{c^{2}} \cdot \frac{c^{2}}{a^{2}}} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
or
$$
\sqrt{3} \leq \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
$$
On the other hand, the Cauchy-Schwarz inequality implies
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+ & \frac{c}{a} \leq \sqrt{1^{2}+1^{2}+1^{2}} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}} \\
& =\sqrt{3} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
\end{aligned}
$$
We arrive at the inequality of the problem by combining (1) and (2).
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 365
|
88.1. The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
|
Solution. If $x=\sqrt[3]{n}$, and $y, 0 \leq y1000$, and $x>31$. On the other hand, $x^{3}<1000 x+1000$, or $x\left(x^{2}-1000\right)<1000$. The left hand side of this inequality is an increasing function of $x$, and $x=33$ does not satisfy the inequality. So $x<33$. Since $x$ is an integer, $x=32$ and $n=32^{3}=32768$.
|
32768
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 366
|
88.2. Let $a, b$, and $c$ be non-zero real numbers and let $a \geq b \geq c$. Prove the inequality
$$
\frac{a^{3}-c^{3}}{3} \geq a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
When does equality hold?
|
Solution. Since $c-b \leq 0 \leq a-b$, we have $(a-b)^{3} \geq(c-b)^{3}$, or
$$
a^{3}-3 a^{2} b+3 a b^{2}-b^{3} \geq c^{3}-3 b c^{2}+3 b^{2} c-b^{3}
$$
On simplifying this, we immediately have
$$
\frac{1}{3}\left(a^{3}-c^{3}\right) \geq a^{2} b-a b^{2}+b^{2} c-b c^{2}=a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
A sufficient condition for equality is $a=c$. If $a>c$, then $(a-b)^{3}>(c-b)^{3}$, which makes the proved inequality a strict one. So $a=c$ is a necessary condition for equality, too.
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 367
|
88.3. Two concentric spheres have radii $r$ and $R, r<R$. We try to select points $A, B$ and $C$ on the surface of the larger sphere such that all sides of the triangle $A B C$ would be tangent to the surface of the smaller sphere. Show that the points can be selected if and only if $R \leq 2 r$.
|
Solution. Assume $A, B$, and $C$ lie on the surface $\Gamma$ of a sphere of radius $R$ and center $O$, and $A B, B C$, and $C A$ touch the surface $\gamma$ of a sphere of radius $r$ and center $O$. The circumscribed and inscribed circles of $A B C$ then are intersections of the plane $A B C$ with $\Gamma$ and $\gamma$, respectively. The centers of these circles both are the foot $D$ of the perpendicular dropped from $O$ to the plane $A B C$. This point lies both on the angle bisectors of the triangle $A B C$ and on the perpendicular bisectors of its sides. So these lines are the same, which means that the triangle $A B C$ is equilateral, and the center of the circles is the common point of intersection of the medians of $A B C$. This again implies that the radii of the two circles are $2 r_{1}$ and $r_{1}$ for some real number $r_{1}$. Let $O D=d$. Then $2 r_{1}=\sqrt{R^{2}-d^{2}}$ and $r_{1}=\sqrt{r^{2}-d^{2}}$. Squaring, we get $R^{2}-d^{2}=4 r^{2}-4 d^{2}, 4 r^{2}-R^{2}=3 d^{2} \geq 0$, and $2 r \geq R$. On the other hand, assume $2 r \geq R$. Consider a plane at the distance
$$
d=\sqrt{\frac{4 r^{2}-R^{2}}{3}}
$$
from the common center of the two spheres. The plane cuts the surfaces of the spheres along concentric circles of radii
$$
r_{1}=\sqrt{\frac{R^{2}-r^{2}}{3}}, \quad R_{1}=2 \sqrt{\frac{R^{2}-r^{2}}{3}}
$$
The points $A, B$, and $C$ can now be chosen on the latter circle in such a way that $A B C$ is equilateral.
|
R\leq2r
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 368
|
88.4. Let $m_{n}$ be the smallest value of the function
$$
f_{n}(x)=\sum_{k=0}^{2 n} x^{k}
$$
Show that $m_{n} \rightarrow \frac{1}{2}$, as $n \rightarrow \infty$.
|
Solution. For $n>1$,
$$
\begin{gathered}
f_{n}(x)=1+x+x^{2}+\cdots \\
=1+x\left(1+x^{2}+x^{4}+\cdots\right)+x^{2}\left(1+x^{2}+x^{4} \cdots\right) \\
=1+x(1+x) \sum_{k=0}^{n-1} x^{2 k}
\end{gathered}
$$
From this we see that $f_{n}(x) \geq 1$, for $x \leq-1$ and $x \geq 0$. Consequently, $f_{n}$ attains its minimum value in the interval $(-1,0)$. On this interval
$$
f_{n}(x)=\frac{1-x^{2 n+1}}{1-x}>\frac{1}{1-x}>\frac{1}{2}
$$
So $m_{n} \geq \frac{1}{2}$. But
$$
m_{n} \leq f_{n}\left(-1+\frac{1}{\sqrt{n}}\right)=\frac{1}{2-\frac{1}{\sqrt{n}}}+\frac{\left(1-\frac{1}{\sqrt{n}}\right)^{2 n+1}}{2-\frac{1}{\sqrt{n}}}
$$
As $n \rightarrow \infty$, the first term on the right hand side tends to the limit $\frac{1}{2}$. In the second term, the factor
$$
\left(1-\frac{1}{\sqrt{n}}\right)^{2 n}=\left(\left(1-\frac{1}{\sqrt{n}}\right)^{\sqrt{n}}\right)^{2 \sqrt{n}}
$$
of the nominator tehds to zero, because
$$
\lim _{k \rightarrow \infty}\left(1-\frac{1}{k}\right)^{k}=e^{-1}<1
$$
So $\lim _{n \rightarrow \infty} m_{n}=\frac{1}{2}$.
89.1 Find a polynomial $P$ of lowest possible degree such that
(a) $P$ has integer coefficients,
(b) all roots of $P$ are integers,
(c) $P(0)=-1$,
(d) $P(3)=128$.
|
\frac{1}{2}
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 369
|
89.2. Three sides of a tetrahedron are right-angled triangles having the right angle at their common vertex. The areas of these sides are $A, B$, and $C$. Find the total surface area of the tetrahedron.
|
Solution 1. Let $P Q R S$ be the tetrahedron of the problem and let $S$ be the vertex common to the three sides which are right-angled triangles. Let the areas of $P Q S, Q R S$, and $R P S$ be $A, B$, and $C$, respectively. Denote the area of $Q R S$ by $X$. If $S S^{\prime}$ is the altitude from $S$ (onto $P Q R$ ) and $\angle R S S^{\prime}=\alpha, \angle P S S^{\prime}=\beta, \angle Q S S^{\prime}=\gamma$, the rectangular parallelepiped with $S S^{\prime}$ as a diameter, gives by double use of the Pythagorean theorem
$$
\begin{gathered}
S S^{\prime 2}=\left(S S^{\prime} \cos \alpha\right)^{2}+\left(S S^{\prime} \sin \alpha\right)^{2} \\
=\left(S S^{\prime} \cos \alpha\right)^{2}+\left(S S^{\prime} \cos \beta\right)^{2}+\left(S S^{\prime} \cos \gamma\right)^{2}
\end{gathered}
$$
or
$$
\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1
$$
(a well-known formula). The magnitude of the dihedral angle between two planes equals the angle between the normals of the planes. So $\alpha, \beta$, and $\gamma$ are the magnitudes of the dihedral angles between $P Q R$ and $P Q S, Q R S$, and $R P S$, respectively. Looking at the projections of $P Q R$ onto the three other sides of $P Q R S$, we get $A=X \cos \alpha, B=X \cos \beta$, and $C=X \cos \gamma$. But (1) now yields $X^{2}=A^{2}+B^{2}+C^{2}$. The total area of $P Q R S$ then equals $A+B+C+\sqrt{A^{2}+B^{2}+C^{2}}$.
|
A+B+C+\sqrt{A^{2}+B^{2}+C^{2}}
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 370
|
89.3. Let $S$ be the set of all points $t$ in the closed interval $[-1,1]$ such that for the sequence $x_{0}, x_{1}, x_{2}, \ldots$ defined by the equations $x_{0}=t, x_{n+1}=2 x_{n}^{2}-1$, there exists a positive integer $N$ such that $x_{n}=1$ for all $n \geq N$. Show that the set $S$ has infinitely many elements.
|
Solution. All numbers in the sequence $\left\{x_{n}\right\}$ lie in the interval $[-1,1]$. For each $n$ we can pick an $\alpha_{n}$ such that $x_{n}=\cos \alpha_{n}$. If $x_{n}=\cos \alpha_{n}$, then $x_{n+1}=2 \cos ^{2} \alpha_{n}-1=\cos \left(2 \alpha_{n}\right)$. The nuber $\alpha_{n+1}$ can be chosen as $2 \alpha_{n}$, and by induction, $\alpha_{n}$ can be chosen as $2^{n} \alpha_{0}$. Now $x_{n}=1$ if and only if $\alpha_{n}=2 k \pi$ for some integer $k$. Take $S^{\prime}=\left\{\cos \left(2^{-m} \pi\right) \mid m \in \mathbb{N}\right\}$. Since every $\alpha_{0}=2^{-m} \pi$ multiplied by a sufficiently large power of 2 is a multiple of $2 \pi$, it follows from what was said above that $S^{\prime} \subset S$. Since $S^{\prime}$ is infinite, so is $S$.
89.4 For which positive integers $n$ is the following statement true: if $a_{1}, a_{2}, \ldots, a_{n}$ are positive integers, $a_{k} \leq n$ for all $k$ and $\sum_{k=1}^{n} a_{k}=2 n$, then it is always possible to choose $a_{i_{1}}, a_{i_{2}}, \ldots, a_{i_{j}}$ in such a way that the indices $i_{1}, i_{2}, \ldots, i_{j}$ are different numbers, and $\sum_{k=1}^{j} a_{i_{k}}=n$ ?
|
notfound
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 371
|
90.1. Let $m, n$, and $p$ be odd positive integers. Prove that the number
$$
\sum_{k=1}^{(n-1)^{p}} k^{m}
$$
is divisible by $n$.
|
Solution. Since $n$ is odd, the sum has an even number of terms. So we can write it as
$$
\sum_{k=1}^{\frac{1}{2}(n-1)^{p}}\left(k^{m}+\left((n-1)^{p}-k+1\right)^{m}\right)
$$
Because $m$ is odd, each term in the sum has $k+(n-1)^{p}-k+1=(n-1)^{p}+1$ as a factor. As $p$ is odd, too, $(n-1)^{p}+1=(n-1)^{p}+1^{p}$ has $(n-1)+1=n$ as a factor. So each term in the sum (1) is divisible by $n$, and so is the sum.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 372
|
90.2. Let $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers. Prove
$$
\sqrt[3]{a_{1}^{3}+a_{2}^{3}+\ldots+a_{n}^{3}} \leq \sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}}
$$
When does equality hold in (1)?
|
Solution. If $0 \leq x \leq 1$, then $x^{3 / 2} \leq x$, and equality holds if and only if $x=0$ or $x=1$. - The inequality is true as an equality, if all the $a_{k}$ 's are zeroes. Assume that at least one of the numbers $a_{k}$ is non-zero. Set
$$
x_{k}=\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}
$$
Then $0 \leq x_{k} \leq 1$, and by the remark above,
$$
\sum_{k=1}^{n}\left(\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}\right)^{3 / 2} \leq \sum_{k=1}^{n} \frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}=1
$$
So
$$
\sum_{k=1}^{n} a_{k}^{3} \leq\left(\sum_{j_{1}}^{n} a_{j}^{2}\right)^{3 / 2}
$$
which is what was supposed to be proved. For equality, exactly on $x_{k}$ has to be one and the rest have to be zeroes, which is equivalent to having exactly one of the $a_{k}$ 's positive and the rest zeroes.
Figure 2.
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 373
|
90.3. Let $A B C$ be a triangle and let $P$ be an interior point of $A B C$. We assume that a line $l$, which passes through $P$, but not through $A$, intersects $A B$ and $A C$ (or their extensions over $B$ or $C$ ) at $Q$ and $R$, respectively. Find $l$ such that the perimeter of the triangle $A Q R$ is as small as possible.
|
Solution. (See Figure 2.) Let
$$
s=\frac{1}{2}(A R+R Q+Q A)
$$
Let $\mathcal{C}$ be the excircle of $A Q R$ tangent to $Q R$, i.e. the circle tangent to $Q R$ and the extensions of $A R$ and $A Q$. Denote the center of $\mathcal{C}$ by $I$ and the measure of $\angle Q A R$ by $\alpha . I$ is on the bisector of $\angle Q A R$. Hence $\angle Q A I=\angle I A R=\frac{1}{2} \alpha$. Let $\mathcal{C}$ touch $R Q$, the extension of $A Q$, and the extension of $A R$ at $X, Y$, and $Z$, respectively. Clearly
$$
A Q+Q X=A Y=A Z=A R+R X
$$
so
$$
A Z=A I \cos \frac{1}{2} \alpha=s
$$
Hence $s$ and the perimeter of $A Q R$ is smallest, when $A I$ is smallest. If $P \neq X$, it is possible to turn the line through $P$ to push $\mathcal{C}$ deeper into the angle $B A C$. So the minumum for $A I$ is achieved precisely as $X=P$. To construct minimal triangle, we have to draw a circle touching the half lines $A B$ and $A C$ and passing through $P$. This is accomplished by first drawing an arbitrary circle touching the half lines, and then performing a suitable homothetic transformation of the circle to make it pass through $P$.
|
notfound
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 374
|
90.4. It is possible to perform three operations $f, g$, and $h$ for positive integers: $f(n)=$ $10 n, g(n)=10 n+4$, and $h(2 n)=n$; in other words, one may write 0 or 4 in the end of the number and one may divide an even number by 2. Prove: every positive integer can be constructed starting from 4 and performing a finite number of the operations $f, g$, and $h$ in some order.
|
Solution. All odd numbers $n$ are of the form $h(2 n)$. All we need is to show that every even number can be obtained fron 4 by using the operations $f, g$, and $h$. To this end, we show that a suitably chosen sequence of inverse operations $F=f^{-1}, G=g^{-1}$, and $H=h^{-1}$ produces a smaller even number or the number 4 from every positive even integer. The operation $F$ can be applied to numbers ending in a zero, the operation $G$ can be applied to numbers ending in 4 , and $H(n)=2 n$. We obtain
$$
\begin{gathered}
H(F(10 n))=2 n \\
G(H(10 n+2))=2 n, \quad n \geq 1 \\
H(2)=4 \\
H(G(10 n+4))=2 n \\
G(H(H(10 n+6)))=4 n+2 \\
G(H(H(H(10 n+8))))=8 n+6
\end{gathered}
$$
After a finite number of these steps, we arrive at 4 .
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 375
|
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
Solution. We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 376
|
91.3. Show that
$$
\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{n^{2}}<\frac{2}{3}
$$
for all $n \geq 2$.
|
Solution. Since
$$
\frac{1}{j^{2}}<\frac{1}{j(j-1)}=\frac{1}{j-1}-\frac{1}{j}
$$
we have
$$
\begin{gathered}
\sum_{j=k}^{n} \frac{1}{j^{2}}<\left(\frac{1}{k-1}-\frac{1}{k}\right)+\left(\frac{1}{k}-\frac{1}{k+1}\right)+\cdots+\left(\frac{1}{n-1}-\frac{1}{n}\right) \\
=\frac{1}{k-1}-\frac{1}{n}<\frac{1}{k-1}
\end{gathered}
$$
From this we obtain for $k=6$
$$
\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{n^{2}}<\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+\frac{1}{5}=\frac{2389}{3600}<\frac{2}{3}
$$
|
\frac{2389}{3600}<\frac{2}{3}
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 378
|
91.4. Let $f(x)$ be a polynomial with integer coefficients. We assume that there exists a positive integer $k$ and $k$ consecutive integers $n, n+1, \ldots, n+k-1$ so that none of the numbers $f(n), f(n+1), \ldots, f(n+k-1)$ is divisible by $k$. Show that the zeroes of $f(x)$ are not integers.
|
Solution. Let $f(x)=a_{0} x^{d}+a_{1} x^{d-1}+\cdots+a_{d}$. Assume that $f$ has a zero $m$ which is an integer. Then $f(x)=(x-m) g(x)$, where $g$ is a polynomial. If $g(x)=b_{0} x^{d-1}+b_{1} x^{d-2}+$ $\cdots+b_{d-1}$, then $a_{0}=b_{0}$, and $a_{k}=b_{k}-m b_{k-1}, 1 \leq k \leq d-1$. So $b_{0}$ is an integer, and by induction all $b_{k}$ 's are integers. Because $f(j)$ is not divisible by $k$ for $k$ consequtive values of $j$, no one of the $k$ consequtive integers $j-m, j=n, n+1, \ldots, n+k-1$, is divisible by $k$. But this is a contradiction, since exactly one of $k$ consequtive integers is divisible by $k$. So $f$ cannot have an integral zero.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 379
|
92.1. Determine all real numbers $x>1, y>1$, and $z>1$, satisfying the equation
$$
\begin{aligned}
x+y+z+\frac{3}{x-1} & +\frac{3}{y-1}+\frac{3}{z-1} \\
& =2(\sqrt{x+2}+\sqrt{y+2}+\sqrt{z+2})
\end{aligned}
$$
|
Solution. Consider the function $f$,
$$
f(t)=t+\frac{3}{t-1}-2 \sqrt{t+2}
$$
defined for $t>1$. The equation of the problem can be written as
$$
f(x)+f(y)+f(z)=0
$$
We reformulate the formula for $f$ :
$$
\begin{aligned}
f(t) & =\frac{1}{t-1}\left(t^{2}-t+3-2(t-1) \sqrt{t+2}\right) \\
& =\frac{1}{t-1}\left(t^{2}-2 t+1+(\sqrt{t+2})^{2}-2(t-1) \sqrt{t+2}\right) \\
& =\frac{1}{t-1}(t-1-\sqrt{t+2})^{2}
\end{aligned}
$$
So $f(t) \geq 0$, and $f(t)=0$ for $t>1$ only if
$$
t-1=\sqrt{t+2}
$$
or
$$
t^{2}-3 t-1=0
$$
The only $t$ satisfying this condition is
$$
t=\frac{3+\sqrt{13}}{2}
$$
So the only solution to the equation in the problem is given by
$$
x=y=z=\frac{3+\sqrt{13}}{2}
$$
|
\frac{3+\sqrt{13}}{2}
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 380
|
92.2. Let $n>1$ be an integer and let $a_{1}, a_{2}, \ldots, a_{n}$ be $n$ different integers. Show that the polynomial
$$
f(x)=\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)-1
$$
is not divisible by any polynomial with integer coefficients and of degree greater than zero but less than $n$ and such that the highest power of $x$ has coefficient 1.
|
Solution. Suppose $g(x)$ is a polynomial of degree $m$, where $1 \leq m<n$, with integer coefficients and leading coefficient 1 , such that
$$
f(x)=g(x) h(x)
$$
whre $h(x)$ is a polynomial. Let
$$
\begin{aligned}
& g(x)=x^{m}+b_{m-1} x^{m-1}+\cdots+b_{1} x+b_{0} \\
& h(x)=x^{n-m}+c_{n-m-1} x^{n-m-1}+\cdots+c_{1} x+c_{0}
\end{aligned}
$$
We show that the coefficients of $h(x)$ are integers. If they are not, there is a greatest index $j=k$ such that $c_{k}$ is not an integer. But then the coefficient of $f$ multiplying $x^{k+m}-$ which is an integer - would be $c_{k}+b_{m-1} c_{k+1}+b_{m-2} c_{k+2}+\ldots b_{k-m}$. All terms except the first one in this sum are integers, so the sum cannot be an integer. A contradiction. So $h(x)$ is a polynomial with integral coefficients. Now
$$
f\left(a_{i}\right)=g\left(a_{i}\right) h\left(a_{i}\right)=-1
$$
for $i=1,2, \ldots, n$, and $g\left(a_{i}\right)$ and $h\left(a_{i}\right)$ are integers. This is only possible, if $g\left(a_{i}\right)=$ $-f\left(a_{i}\right)= \pm 1$ and $g\left(a_{i}\right)+h\left(a_{i}\right)=0$ for $i=1,2, \ldots, n$. So the polynomial $g(x)+h(x)$ has at least $n$ zeroes. But the degree of $g(x)+h(x)$ is less than $n$. So $g(x)=-h(x)$ for all $x$, and $f(x)=-g(x)^{2}$. This is impossible, however, because $f(x) \rightarrow+\infty$, as $x \rightarrow+\infty$. This contradiction proves the claim.
Figure 4 .
92.3 Prove that among all triangles with inradius 1, the equilateral one has the smallest perimeter.
|
proof
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 381
|
92.4. Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
Solution. We show that Peter only can make a $4 \times 4$ square. The construction is possible, if $n=4$ :

Now consider the case $n=5$. We may assume that at least 13 of the 25 squares are black. If five black squares are on one horizontal row, the remaining eight ones are distributed on the other four rows. At least one row has two black squres. A rectangle with all corners black is created. Next assume that one row has four black squares. Of the remaing 9 squares, at least three are one row. At least two of these three have to be columns having the assumed four black squares. If no row has more than four black squares, there have to be at least three rows with exactly three black squares. Denote these rows by $A, B$, and $C$. Let us call the columns in which the black squares on row $A$ lie black columns, and the other two columns white columns. If either row $B$ or row $C$ has at least two black squares which are on black columns, a rectancle with black corners arises. If both rows $B$ and $C$ have only one black square on the black columns, then both of them have two black squares on the two white columns, and they make the black corners of a rectangle. So Peter cannot make a $5 \times 5$ square in the way he wishes.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 382
|
93.1. Let $F$ be an increasing real function defined for all $x, 0 \leq x \leq 1$, satisfying the conditions
$$
\begin{aligned}
& F\left(\frac{x}{3}\right)=\frac{F(x)}{2} \\
& F(1-x)=1-F(x)
\end{aligned}
$$
Determine $F\left(\frac{173}{1993}\right)$ and $F\left(\frac{1}{13}\right)$.
|
Solution. Condition (i) implies $F(0)=\frac{1}{2} F(0)$, so $F(0)=0$. Because of condition (ii), $F(1)=1-F(0)=1$. Also $F\left(\frac{1}{3}\right)=\frac{1}{2}$ and $F\left(\frac{2}{3}\right)=1-F\left(\frac{1}{3}\right)=\frac{1}{2}$. Since $F$ is an increasing function, this is possible only if $F(x)=\frac{1}{2}$ for all $x \in\left[\frac{1}{3}, \frac{2}{3}\right]$. To determine the first of the required values of $F$, we use (i) and (ii) to transform the argument into the middle third of $[0,1]$ :
$$
F\left(\frac{173}{1993}\right)=\frac{1}{2} F\left(\frac{519}{1993}\right)=\frac{1}{4} F\left(\frac{1557}{1993}\right)
$$
$$
\begin{gathered}
=\frac{1}{4}\left(1-F\left(\frac{436}{1993}\right)\right)=\frac{1}{4}\left(1-\frac{1}{2} F\left(\frac{1308}{1993}\right)\right) \\
=\frac{1}{4}\left(1-\frac{1}{4}\right)=\frac{3}{16}
\end{gathered}
$$
To find the second value of $F$, we use (i) and (ii) to form an equation fron which the value can be solved. Indeed,
$$
\begin{gathered}
F\left(\frac{1}{13}\right)=1-F\left(\frac{12}{13}\right)=1-2 F\left(\frac{4}{13}\right) \\
=1-2\left(1-F\left(\frac{9}{13}\right)\right)=2 F\left(\frac{9}{13}\right)-1=4 F\left(\frac{3}{13}\right)-1 \\
=8 F\left(\frac{1}{13}\right)-1
\end{gathered}
$$
From this we solve
$$
F\left(\frac{1}{13}\right)=\frac{1}{7}
$$
|
\frac{3}{16},\frac{1}{7}
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 383
|
93.2. A hexagon is inscribed in a circle of radius $r$. Two of the sides of the hexagon have length 1, two have length 2 and two have length 3. Show that $r$ satisfies the equation
$$
2 r^{3}-7 r-3=0
$$
Figure 5.
|
Solution. (See Figure 5.) We join the vertices of the hexagon to the center $O$ of its circumcircle. We denote by $\alpha$ the central angles corresponding the chords of length 1 , by $\beta$ those corresponding the chords of length 2 , and by $\gamma$ those corresponding the chords of length 3. Clearly $\alpha+\beta+\gamma=180^{\circ}$. We can move three chords of mutually different length so that they follow each other on the circumference. We thus obtain a quadrilateral $A B C D$ where $A B=2 r$ is a diameter of the circle, $B C=1, C D=2$, and $D A=3$. Then
$\angle C O B=\alpha$ and $\angle C A B=\frac{\alpha}{2}$. Then $\angle A B C=90^{\circ}-\frac{\alpha}{2}$, and, as $A B C D$ is an inscribed quafdrilateral, $\angle C D A=90^{\circ}+\frac{\alpha}{2}$. Set $A C=x$. From triangles $A B C$ and $A C D$ we obtain $x^{2}+1=4 r^{2}$ and
$$
x^{2}=4+9-2 \cdot 2 \cdot 3 \cos \left(90^{\circ}+\frac{\alpha}{2}\right)=13+12 \sin \left(\frac{\alpha}{2}\right)
$$
From triangle $A B C$,
$$
\sin \left(\frac{\alpha}{2}\right)=\frac{1}{2 r}
$$
We put this in the expression for $x^{2}$ to obtain
$$
4 r^{2}=x^{2}+1=14+12 \cdot \frac{1}{2 r}
$$
which is equivalent to
$$
2 r^{3}-7 r-3=0
$$
|
2r^{3}-7r-3=0
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 384
|
93.3. Find all solutions of the system of equations
$$
\left\{\begin{aligned}
s(x)+s(y) & =x \\
x+y+s(z) & =z \\
s(x)+s(y)+s(z) & =y-4
\end{aligned}\right.
$$
where $x, y$, and $z$ are positive integers, and $s(x), s(y)$, and $s(z)$ are the numbers of digits in the decimal representations of $x, y$, and $z$, respectively.
|
Solution. The first equation implies $x \geq 2$ and the first and third equation together imply
$$
s(z)=y-x-4
$$
So $y \geq x+5 \geq 7$. From (1) and the second equation we obtain $z=2 y-4$. Translated to the values of $s$, these equation imply $s(x) \leq s(2 y) \leq s(y)+1$ and $s(x) \leq s(y)$. We insert these inequalitien in the last equation of the problem to obtain $y-4 \leq 3 s(y)+1$ or $y \leq 3 s(y)+5$. Since $10^{s(y)-1} \leq y$, the only possible values of $s(y)$ are 1 and 2 . If $s(y)=1$, then $7 \leq y \leq 3+5=8$. If $y=7, x$ must be 2 and $z=2 \cdot 7-4=10$. But this does not fit in the second equation: $2+7+2 \neq 10$. If $y=8$, then $z=12, x=2$. The triple $(2,8,12)$ satisfies all the equations of the problem. If $s(y)=2$, then $y \leq 6+5=11$. The only possibilities are $y=10$ and $y=11$. If $y=10$, then $z=16$ and $x \leq 5$. The equation $s(x)+s(y)+s(z)=y-4=6$ is not satisfied. If $y=11$, then $z=18$ and $x \leq 6$. Again, the third equation is not satisfied. So $x=2, y=8$, and $z=12$ is the only solution.
|
(2,8,12)
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 385
|
93.4. Denote by $T(n)$ the sum of the digits of the decimal representation of a positive integer $n$.
a) Find an integer $N$, for which $T(k \cdot N)$ is even for all $k, 1 \leq k \leq 1992$, but $T(1993 \cdot N)$ is odd.
b) Show that no positive integer $N$ exists such that $T(k \cdot N)$ is even for all positive integers $k$.
|
Solution. a) If $s$ has $n$ decimal digits and $m=10^{n+r} s+s$, then $T(k m)$ is even at least as long as $k s<10^{n+r}$, because all non-zero digits appear in pairs in $k m$. Choose $N=5018300050183$ or $s=50183, n=5, r=3$. Now $1992 \cdot s=99964536<10^{8}$, so $T(k N)$ is even for all $k \leq 1992$. But $1993 \cdot s=100014719,1993 \cdot N=10001472000014719$, and $T(1993 \cdot N)=39$ is odd.
b) Assume that $N$ is a positive integer for which $T(k N)$ is even for all $k$. Consider the case $N=2 m$ first. Then $T(k m)=T(10 k m)=T(5 k N)$. As $T(5 k N)$ is even for every $k$, then so is $T(k m)$. Repeating the argument suffiently many times we arrive at an odd $N$, such that $T(k N)$ is even for all $k$. Assume now $N=10 r+5$. Then $T(k(2 r+1))=T(10 k(2 r+1))=$ $T(2 k N)$. From this we conclude that the number $\frac{N}{5}=2 r+1$ has the the property we are dealing with. By repeating the argument, we arrive at an odd number $N$, which does not have 5 as a factor, such that $T(k N)$ is even for all $k$. Next assume $N=10 r+9$. If $N$ has $n$ digits and the decimal representation of $N$ is $\overline{a x \ldots x b 9}$, where the $x$ 's can be any digits, then, if $b<9$, the decimal representation of $10^{n-1} N+N$ is $\overline{a x \ldots x(b+1)(a-1) x \ldots x b 9}$. This implies $T\left(10^{n-2} N+N\right)=2 T(N)-9$, which is an odd number. If the second last digit $b$ of $N$ is 9 , then $11 N$ has 89 as its two last digits, and again we see that $N$ has a multiple $k N$ with $T(k n)$ odd. Finally, if the last digit of $N$ is 1 , the last digit of $9 N$ is 9 , if the last digit of $N$ is 3 , the last digit of $3 N$ is 9 , and if the last digit of $N$ is 7 , the last digit of $7 N$ is 9 . All these cases thus can be reduced to the cases already treated. So all odd numbers have multiples with an odd sum of digits, and the proof is complete.
|
proof
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 386
|
94.1. Let $O$ be an interior point in the equilateral triangle $A B C$, of side length $a$. The lines $A O, B O$, and $C O$ intersect the sides of the triangle in the points $A_{1}, B_{1}$, and $C_{1}$. Show that
$$
\left|O A_{1}\right|+\left|O B_{1}\right|+\left|O C_{1}\right|<a
$$
|
Solution. Let $H_{A}, H_{B}$, and $H_{C}$ be the orthogonal projections of $O$ on $B C, C A$, and $A B$, respectively. Because $60^{\circ}\left|O A_{1}\right| \frac{\sqrt{3}}{2}
$$
In the same way,
$$
\left|O H_{B}\right|>\left|O B_{1}\right| \frac{\sqrt{3}}{2} \quad \text { and } \quad\left|O H_{C}\right|>\left|O C_{1}\right| \frac{\sqrt{3}}{2}
$$
The area of $A B C$ is $a^{2} \frac{\sqrt{3}}{4}$ but also $\frac{a}{2}\left(O H_{A}+O H_{B}+O H_{C}\right)$ (as the sum of the areas of the three triangles with common vertex $O$ which together comprise $A B C$ ). So
$$
\left|O H_{A}\right|+\left|O H_{B}\right|+\left|O H_{C}\right|=a \frac{\sqrt{3}}{2}
$$
and the claim follows at once.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 387
|
94.2. We call a finite plane set $S$ consisting of points with integer coefficients a twoneighbour set, if for each point $(p, q)$ of $S$ exactly two of the points $(p+1, q),(p, q+1)$, $(p-1, q),(p, q-1)$ belong to $S$. For which integers $n$ there exists a two-neighbour set which contains exactly $n$ points?
|
Solution. The points $(0,0),(1,0),(1,1),(0,1)$ clearly form a two-neighbour set (which we abbreviate as $2 \mathrm{NS})$. For every even number $n=2 k \geq 8$, the set $S=\{(0,0), \ldots$, $(k-2,0),(k-2,1),(k-2,2), \ldots,(0,2),(0,1)\}$ is a $2 \mathrm{NS}$. We show that there is no $2 \mathrm{NS}$ with $n$ elements for other values $n$.
Assume that $S$ is a $2 \mathrm{NS}$ and $S$ has $n$ points. We join every point in $S$ to two of its neighbours by a unit line segment. The ensuing figures are closed polygonal lines, since an end-point of such a line would have only one neighbour. The polygons contains altogether $n$ segments (from each point, two segments emanate, and counting the emanating segments means that the segments will be counted twice.) In each of the polygons, the number of segments is even. When walking around such a polygon one has to take equally many steps to the left as to the right, and equally many up and down. Also, $n \neq 2$.
What remains is to show is that $n \neq 6$. We may assume $(0,0) \in S$. For reasons of symmetry, essentially two possibilities exist: a) $(-1,0) \in S$ and $(1,0) \in S$, or b) $(1,0) \in S$ and $(0,1) \in S$. In case a), $(0,1) \notin S$ and $(0,-1) \notin S$. Because the points $(-1,0),(0,0)$, and $(1,0)$ of $S$ belong to a closed polygonal line, this line has to wind around either $(0,1)$ or $(0,-1)$. In both cases, the polygon has at least 8 segments. In case b) $(1,1) \notin S$ (because otherwise $S$ would generate two polygons, a square an one with two segments). Also $(-1,0) \notin S$, and $(0,-1) \notin S$. The polygon which contains $(1,0),(0,0)$, and $(0,1)$ thus either winds around the point $(1,1)$, in which case it has at least 8 segments, or it turns around the points $(-1,0)$ and $(0,-1)$, in which case it has at least 10 segments. So $n=6$ always leads to a contradiction.
|
proof
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 388
|
94.3. A piece of paper is the square $A B C D$. We fold it by placing the vertex $D$ on the point $H$ of the side $B C$. We assume that $A D$ moves onto the segment $G H$ and that $H G$ intersects $A B$ at $E$. Prove that the perimeter of the triangle $E B H$ is one half of the perimeter of the square.
Figure 6 .
|
Solution. (See Figure 6.) The fold gives rise to an isosceles trapezium $A D H G$. Because of symmetry, the distance of the vertex $D$ from the side $G H$ equals the distance of the vertex
$H$ from side $A D$; the latter distance is the side length $a$ of the square. The line $G H$ thus is tangent to the circle with center $D$ and radius $a$. The lines $A B$ and $B C$ are tangent to the same circle. If the point common to $G H$ and the circle is $F$, then $A E=E F$ and $F H=H C$. This implies $A B+B C=A E+E B+B H+H C=E F+E B+B H+H F=E H+E B+B H$, which is equivalent to what we were asked to prove.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 389
|
94.4. Determine all positive integers $n<200$, such that $n^{2}+(n+1)^{2}$ is the square of an integer.
|
Solution. We determine the integral solutions of
$$
n^{2}+(n+1)^{2}=(n+p)^{2}, \quad p \geq 2
$$
The root formula for quadratic equations yields
$$
n=p-1+\sqrt{2 p(p-1)} \geq 2(p-1)
$$
Because $n<200$, we have $p \leq 100$. Moreover, the number $2 p(p-1)$ has to be the square of an integer. If $p$ is odd, $p$ and $2(p-1)$ have no common factors. Consequently, both $p$ and $2(p-1)$ have to be squares. The only possible candidates are $p=9, p=25, p=49$, $p=81$. The respective numbers $2(p-1)$ are $16,48,96$, and 160 . Of these, only 16 is a square. We thus have one solution $n=8+\sqrt{2 \cdot 9 \cdot 8}=20,20^{2}+21^{2}=841=29^{2}$. If $p$ is even, the numbers $2 p$ and $p-1$ have no factors in common, so both are squares. Possible candidates for $2 p$ are $4,16,36,64,100,144$, and 196. The corresponding values of $p-1$ are $1,7,31,49,71,97$. We obtain two more solutions: $n=1+2=3,3^{2}+4^{2}=5^{2}$, and $n=49+70=119,119^{2}+120^{2}=169^{2}$.
|
20,3,119
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 390
|
95.1. Let $A B$ be a diameter of a circle with centre $O$. We choose a point $C$ on the circumference of the circle such that $O C$ and $A B$ are perpendicular to each other. Let $P$ be an arbitrary point on the (smaller) arc $B C$ and let the lines $C P$ and $A B$ meet at $Q$. We choose $R$ on $A P$ so that $R Q$ and $A B$ are perpendicular to each other. Show that $|B Q|=|Q R|$.
Figure 7 .
|
Solution 1. (See Figure 7.) Draw $P B$. By the Theorem of Thales, $\angle R P B=\angle A P B=$ $90^{\circ}$. So $P$ and $Q$ both lie on the circle with diameter $R B$. Because $\angle A O C=90^{\circ}$, $\angle R P Q=\angle C P A=45^{\circ}$. Then $\angle R B Q=45^{\circ}$, too, and $R B Q$ is an isosceles right triangle, or $|B Q|=|Q R|$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 391
|
95.2. Messages are coded using sequences consisting of zeroes and ones only. Only sequences with at most two consecutive ones or zeroes are allowed. (For instance the sequence 011001 is allowed, but 011101 is not.) Determine the number of sequences consisting of exactly 12 numbers.
|
Solution 1. Let $S_{n}$ be the set of acceptable sequences consisting of $2 n$ digits. We partition $S_{n}$ in subsets $A_{n}, B_{n}, C_{n}$, and $D_{n}$, on the basis of the two last digits of the sequence. Sequences ending in 00 are in $A_{n}$, those ending in 01 are in $B_{n}$, those ending in 10 are in $C_{n}$, and those ending in 11 are in $D_{n}$. Denote by $x_{n}, a_{n}, b_{n}, c_{n}$, and $d_{n}$ the number of elements in $S_{n}, A_{n}, B_{n}, C_{n}$, and $D_{n}$. We compute $x_{6}$. Because $S_{1}=\{00,01,10,11\}$, $x_{1}=4$ and $a_{1}=b_{1}=c_{1}=d_{1}=1$. Every element of $A_{n+1}$ can be obtained in a unique manner from an element of $B_{n}$ or $D_{n}$ by adjoining 00 to the end. So $a_{n+1}=b_{n}+d_{n}$. The elements of $B_{n+1}$ are similarly obtained from elements of $B_{n}, C_{n}$, and $D_{n}$ by adjoining 01 to the end. So $b_{n+1}=b_{n}+c_{n}+d_{n}$. In a similar manner we obtain the recursion formulas $c_{n+1}=a_{n}+b_{n}+c_{n}$ and $d_{n+1}=a_{n}+c_{n}$. So $a_{n+1}+d_{n+1}=\left(b_{n}+d_{n}\right)+\left(a_{n}+c_{n}\right)=x_{n}$ and $x_{n+1}=2 a_{n}+3 b_{n}+3 c_{n}+2 d_{n}=3 x_{n}-\left(a_{n}+b_{n}\right)=3 x_{n}-x_{n-1}$. Starting from the initial values $a_{1}=b_{1}=c_{1}=d_{1}=1$, we obtain $a_{2}=d_{2}=2, b_{2}=c_{2}=3$, and $x_{2}=10$. So $x_{3}=3 x_{2}-x_{1}=3 \cdot 10-4=26, x_{4}=3 \cdot 26-10=68, x_{5}=3 \cdot 68-26=178$, and $x_{6}=3 \cdot 178-68=466$.
|
466
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 392
|
95.3. Let $n \geq 2$ and let $x_{1}, x_{2}, \ldots x_{n}$ be real numbers satisfying $x_{1}+x_{2}+\ldots+x_{n} \geq 0$ and $x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}=1$. Let $M=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$. Show that
$$
M \geq \frac{1}{\sqrt{n(n-1)}}
$$
When does equality hold in (1)?
|
Solution. Denote by $I$ the set of indices $i$ for which $x_{i} \geq 0$, and by $J$ the set of indices $j$ for which $x_{j}<0$. Let us assume $M<\frac{1}{\sqrt{n(n-1)}}$. Then $I \neq\{1,2, \ldots, n\}$, since otherwise we would have $\left|x_{i}\right|=x_{i} \leq \frac{1}{\sqrt{n(n-1)}}$ for every $i$, and $\sum_{i=1}^{n} x_{i}^{2}<\frac{1}{n-1} \leq 1$. So $\sum_{i \in I} x_{i}^{2}<(n-1) \cdot \frac{1}{n(n-1)}=\frac{1}{n}$, and $\sum_{i \in I} x_{i}<(n-1) \frac{1}{\sqrt{n(n-1)}}=\sqrt{\frac{n-1}{n}}$. Because
$$
0 \leq \sum_{i=1}^{n} x_{i}=\sum_{i \in I} x_{i}-\sum_{i \in J}\left|x_{i}\right|
$$
we must have $\sum_{i \in J}\left|x_{i}\right| \leq \sum_{i \in I} x_{i}<\sqrt{\frac{n-1}{n}}$ and $\sum_{i \in J} x_{i}^{2} \leq\left(\sum_{i \in J}\left|x_{i}\right|\right)^{2}<\frac{n-1}{n}$. But then
$$
\sum_{i=1}^{n} x_{i}^{2}=\sum_{i \in I} x_{i}^{2}+\sum_{i \in J} x_{i}^{2}<\frac{1}{n}+\frac{n-1}{n}=1
$$
and we have a contradiction. - To see that equality $M=\frac{1}{\sqrt{n(n-1)}}$ is possible, we choose $x_{i}=\frac{1}{\sqrt{n(n-1)}}, i=1,2, \ldots, n-1$, and $x_{n}=-\sqrt{\frac{n-1}{n}}$. Now
$$
\sum_{i=1}^{n} x_{i}=(n-1) \frac{1}{\sqrt{n(n-1)}}-\sqrt{\frac{n-1}{n}}=0
$$
and
$$
\sum_{i=1}^{n} x_{i}^{2}=(n-1) \cdot \frac{1}{n(n-1)}+\frac{n-1}{n}=1
$$
We still have to show that equality can be obtained only in this case. Assume $x_{i}=$ $\frac{1}{\sqrt{n(n-1)}}$, for $i=1, \ldots, p, x_{i} \geq 0$, for $i \leq q$, and $x_{i}<0$, kun $q+1 \leq i \leq n$. As before we get
$$
\sum_{i=1}^{q} x_{i} \leq \frac{q}{\sqrt{n(n-1)}}, \quad \sum_{i=q+1}^{n}\left|x_{i}\right| \leq \frac{q}{\sqrt{n(n-1)}}
$$
and
$$
\sum_{i=q+1}^{n} x_{i}^{2} \leq \frac{q^{2}}{n(n-1)}
$$
so
$$
\sum_{i=1}^{n} x_{i}^{2} \leq \frac{q+q^{2}}{n^{2}-n}
$$
It is easy to see that $q^{2}+q<n^{2}+n$, for $n \geq 2$ and $q \leq n-2$, but $(n-1)^{2}+(n-1)=n^{2}-n$. Consequently, a necessary condition for $M=\frac{1}{\sqrt{n(n-1)}}$ is that the sequence only has one negative member. But if among the positive members there is at least one smaller than $M$ we have
$$
\sum_{i=1}^{n}<\frac{q+q^{2}}{n(n-1)}
$$
so the conditions of the problem are not satisfied. So there is equality if and only if $n-1$ of the numbers $x_{i}$ equal $\frac{1}{\sqrt{n(n-1)}}$, and the last one is $\frac{1-n}{\sqrt{n(n-1)}}$.
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 393
|
95.4. Show that there exist infinitely many mutually non-congruent triangles $T$, satisfying
(i) The side lengths of $T$ are consecutive integers.
(ii) The area of $T$ is an integer.
|
Solution. Let $n \geq 3$, and let $n-1, n, n+1$ be the side lengths of the triangle. The semiperimeter of the triangle then equals on $\frac{3 n}{2}$. By Heron's formula, the area of the triangle is
$$
\begin{gathered}
T=\sqrt{\frac{3 n}{2} \cdot\left(\frac{3 n}{2}-n+1\right)\left(\frac{3 n}{2}-n\right)\left(\frac{3 n}{2}-n-1\right)} \\
=\frac{n}{2} \sqrt{\frac{3}{4}\left(n^{2}-4\right)} .
\end{gathered}
$$
If $n=4$, then $T=6$. So at least one triangle of the kind required exists. We prove that we always can form new triangles of the required kind from ones already known to exist. Let $n$ be even, $n \geq 4$, and let $\frac{3}{4}\left(n^{2}-4\right)$ be a square number. Set $m=n^{2}-2$. Then $m>n$, $m$ is even, and $m^{2}-4=(m+2)(m-2)=n^{2}\left(n^{2}-4\right)$. So $\frac{3}{4}\left(m^{2}-4\right)=n^{2} \cdot \frac{3}{4}\left(n^{2}-4\right)$ is a square number. Also, $T=\frac{m}{2} \sqrt{\frac{3}{4}\left(m^{2}-4\right)}$ is an integer. The argument is complete.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 394
|
96.1. Show that there exists an integer divisible by 1996 such that the sum of the its decimal digits is 1996 .
|
Solution. The sum of the digits of 1996 is 25 and the sum of the digits of $2 \cdot 1996=3992$ is 23 . Because $1996=78 \cdot 25+46$, the number obtained by writing 781996 's and two 3992 in succession satisfies the condition of the problem. - As $3 \cdot 1996=5998$, the sum of the digits of 5988 is 30 , and $1996=65 \cdot 30+46$, the number $39923992 \underbrace{5988 \ldots 5988}_{65 \text { times }}$ also can be be given as an answer, indeed a better one, as it is much smaller than the first suggestion.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 395
|
96.2. Determine all real numbers $x$, such that
$$
x^{n}+x^{-n}
$$
is an integer for all integers $n$.
|
Solution. Set $f_{n}(x)=x^{n}+x^{-n}$. $f_{n}(0)$ is not defined for any $n$, so we must have $x \neq 0$. Since $f_{0}(x)=2$ for all $x \neq 0$, we have to find out those $x \neq 0$ for which $f_{n}(x)$ is an integer foe every $n>0$. We note that
$$
x^{n}+x^{-n}=\left(x+x^{-1}\right)\left(x^{n-1}+x^{1-n}\right)-\left(x^{n-2}+x^{2-n}\right)
$$
From this we obtain by induction that $x^{n}+x^{-n}$ is an integer for all $n>1$ as soon as $x+x^{-1}$ is an integer. So $x$ has to satisfy
$$
x+x^{-1}=m
$$
where $m$ is an integer. The roots of this quadratic equation are
$$
x=\frac{m}{2} \pm \sqrt{\frac{m^{2}}{4}-1}
$$
and they are real, if $m \neq-1,0,1$.
|
\frac{}{2}\
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 396
|
96.3. The circle whose diameter is the altitude dropped from the vertex $A$ of the triangle $A B C$ intersects the sides $A B$ and $A C$ at $D$ and $E$, respectively $(A \neq D, A \neq E)$. Show that the circumcentre of $A B C$ lies on the altitude dropped from the vertex $A$ of the triangle $A D E$, or on its extension.
Figure 8.
|
Solution. (See Figure 8.) Let $A F$ be the altitude of $A B C$. We may assume that $\angle A C B$ is sharp. From the right triangles $A C F$ and $A F E$ we obtain $\angle A F E=\angle A C F . \angle A D E$ and $\angle A F E$ subtend the same arc, so they are equal. Thus $\angle A C B=\angle A D E$, and the triangles $A B C$ and $A E D$ are similar. Denote by $P$ and $Q$ the circumcenters of $A B C$ and $A E D$, respectively. Then $\angle B A P=\angle E A Q$. If $A G$ is the altitude of $A E D$, then $\angle D A G=\angle C A F$. But this implies $\angle B A P=\angle D A G$, which means that $P$ is on the altitude $A G$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 397
|
96.4. The real-valued function $f$ is defined for positive integers, and the positive integer a satisfies
$$
\begin{gathered}
f(a)=f(1995), \quad f(a+1)=f(1996), \quad f(a+2)=f(1997) \\
f(n+a)=\frac{f(n)-1}{f(n)+1} \quad \text { for all positive integers } n
\end{gathered}
$$
(i) Show that $f(n+4 a)=f(n)$ for all positive integers $n$.
(ii) Determine the smallest possible $a$.
|
Solution. To prove (i), we the formula $f(n+a)=\frac{f(n)-1}{f(n)+1}$ repeatedly:
$$
\begin{gathered}
f(n+2 a)=f((n+a)+a)=\frac{\frac{f(n)-1}{f(n)+1}-1}{\frac{f(n)-1}{f(n)+1}+1}=-\frac{1}{f(n)} \\
f(n+4 a)=f((n+2 a)+2 a)=-\frac{1}{-\frac{1}{f(n)}}=f(n)
\end{gathered}
$$
(ii) If $a=1$, then $f(1)=f(a)=f(1995)=f(3+498 \cdot 4 a)=f(3)=f(1+2 a)=-\frac{1}{f(1)}$. This clearly is not possible, since $f(1)$ and $\frac{1}{f(1)}$ have equal sign. So $a \neq 1$.
If $a=2$, we obtain $f(2)=f(a)=f(1995)=f(3+249 \cdot 4 a)=f(3)=f(a+1)=f(1996)=$ $f(4+249 \cdot 4 a)=f(4)=f(2+a)=\frac{f(2)-1}{f(2)+1}$, or $f(2)^{2}+f(2)=f(2)-1$. This quadratic equation in $f(2)$ has no real solutions. So $a \neq 2$.
If $a=3$, we try to construct $f$ by choosing $f(1), f(2)$, and $f(3)$ arbitrarily and by computing the other values of $f$ by the recursion formula $f(n+3)=\frac{f(n)-1}{f(n)+1}$. We have to check that $f$ defined in this way satisfies the conditions of the problem.
The condition
$$
f(n+a)=f(n+3)=\frac{f(n)-1}{f(n)+1}
$$
is valid because of the construction. Further, by (i),
$$
f(n+12)=f(n+4 a)=f(n)
$$
which implies
$$
\begin{gathered}
f(a)=f(3)=f(3+166 \cdot 12)=f(1995) \\
f(a+1)=f(4)=f(4+166 \cdot 12)=f(1996) \\
f(a+2)=f(5)=f(5+166 \cdot 12)=f(1997)
\end{gathered}
$$
as required.
We remark that the choice $f(n)=-1$ makes $f(n+3)$ undefined, the choice $f(n)=0$ makes $f(n+3)=-1$ and $f(n+6)$ is undefined, and $f(n)=1$ makes $f(n+3)=0$ so $f(n+9)$ is undefined. In the choice of $f(1), f(2)$, and $f(3)$ we have to avoid $-1,0,1$.
In conclusion, we see that $a=3$ is the smallest possible value for $a$.
|
3
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 398
|
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
Solution. Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 399
|
97.2. Let $A B C D$ be a convex quadrilateral. We assume that there exists a point $P$ inside the quadrilateral such that the areas of the triangles $A B P, B C P, C D P$, and $D A P$ are equal. Show that at least one of the diagonals of the quadrilateral bisects the other diagonal.
Figure 9.
|
Solution. (See Figure 9.) We first assume that $P$ does not lie on the diagonal $A C$ and the line $B P$ meets the diagonal $A C$ at $M$. Let $S$ and $T$ be the feet of the perpendiculars from $A$ and $C$ on the line $B P$. The triangles $A P B$ and $C B P$ have equal area. Thus $A S=C T$. If $S \neq T$, then the right trianges $A S M$ and $C T M$ are congruent, and $A M=C M$. If, on the other hand, $S=T$, the $A C \perp P B$ and $S=M=T$, and again $A M=C M$. In both cases $M$ is the midpoint of the diagonal $A C$. We prove exactly in the same way that the line $D P$ meets $A C$ at the midpoint of $A C$, i.e. at $M$. So $B, M$, and $P$, and also $D, M$, and $P$ are collinear. So $M$ is on the line $D B$, which means that $B D$ divides the diagonal $A C$ in two equal parts.
We then assume that $P$ lies on the diagonal $A C$. Then $P$ is the midpoint of $A C$. If $P$ is not on the diagonal $B D$, we argue as before that $A C$ divides $B D$ in two equal parts. If $P$ lies also on the diagonal $B D$, it has to be the common midpoint of the diagonals.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 400
|
97.3. Let $A, B, C$, and $D$ be four different points in the plane. Three of the line segments $A B, A C, A D, B C, B D$, and $C D$ have length a. The other three have length $b$, where $b>a$. Determine all possible values of the quotient $\frac{b}{a}$.
|
Solution. If the three segments of length $a$ share a common endpoint, say $A$, then the other three points are on a circle of radius $a$, centered at $A$, and they are the vertices of an equilateral triangle of side length $b$. But this means that $A$ is the center of the triangle $B C D$, and
$$
\frac{b}{a}=\frac{b}{\frac{2}{3} \frac{\sqrt{3}}{2} b}=\sqrt{3}
$$
Assume then that of the segments emanating from $A$ at least one has lenght $a$ and at least one has length $b$. We may assume $A B=a$ and $A D=b$. If only one segment of length $a$ would emanate from each of the four poits, then the number of segments of length $a$ would be two, as every segment is counted twice when we count the emanating segments. So we may assume that $A C$ has length $a$, too. If $B C=a$, then $A B C$ would be an equilateral triangle, and the distance of $D$ from each of its vertices would be $b$. This is not possible, since $b>a$. So $B C=b$. Of the segments $C D$ and $B D$ one has length $a$. We may assume $D C=a$. The segments $D C$ and $A B$ are either on one side of thye line $A C$ or on opposite sides of it. In the latter case, $A B C D$ is a parallelogram with a pair of sides of length $a$ and a pair of sides of length $b$, and its diagonals have lengths $a$ and $b$. This is not possible, due to the fact that the sum of the squares of the diagonals of the parallelogram, $a^{2}+b^{2}$, would be equal to the sum of the squares of its sides, i.e. $2 a^{2}+2 b^{2}$. This means that we may assume that $B A C D$ is a convex quadrilateral. Let $\angle A B C=\alpha$ and $\angle A D B=\beta$. From isosceles triangles we obtain for instance $\angle C B D=\beta$, and from the triangle $A B D$ in particular $2 \alpha+2 \beta+\beta=\pi$ as well as $\angle C D A=\alpha, \angle D C B=\frac{1}{2}(\pi-\beta), \angle C A D=\alpha$. The triangle $A D C$ thus yields $\alpha+\alpha+\alpha+\frac{1}{2}(\pi-\beta)=\pi$. From this we solve $\alpha=\frac{1}{5} \pi=36^{\circ}$. The sine theorem applied to $A B C$ gives
$$
\frac{b}{a}=\frac{\sin 108^{\circ}}{\sin 36^{\circ}}=\frac{\sin 72^{\circ}}{\sin 36^{\circ}}=2 \cos 36^{\circ}=\frac{\sqrt{5}+1}{2}
$$
(In fact, $a$ is the side of a regular pentagon, and $b$ is its diagonal.) - Another way of finding the ratio $\frac{b}{a}$ is to consider the trapezium $C D B A$, with $C D \| A B$; if $E$ is the orthogonal projection of $B$ on the segment $C D$, then $C E=b-\frac{1}{2}(b-a)=\frac{1}{2}(b+a)$. The right triangles $B C E$ and $D C E$ yield $C E^{2}=b^{2}-\left(\frac{b+a}{2}\right)^{2}=a^{2}-\left(\frac{b-a}{2}\right)^{2}$, which can be written as $b^{2}-a b-a^{2}=0$. From this we solve $\frac{b}{a}=\frac{\sqrt{5}+1}{2}$.
|
\frac{\sqrt{5}+1}{2}
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 401
|
97.4. Let $f$ be a function defined in the set $\{0,1,2, \ldots\}$ of non-negative integers, satisfying $f(2 x)=2 f(x), f(4 x+1)=4 f(x)+3$, and $f(4 x-1)=2 f(2 x-1)-1$. Show that $f$ is an injection, i.e. if $f(x)=f(y)$, then $x=y$.
|
Solution. If $x$ is even, then $f(x)$ is even, and if $x$ is odd, then $f(x)$ is odd. Moreover, if $x \equiv 1 \bmod 4$, then $f(x) \equiv 3 \bmod 4$, and if $x \equiv 3 \bmod 4$, then $f(x) \equiv 1 \bmod 4$. Clearly $f(0)=0, f(1)=3, f(2)=6$, and $f(3)=5$. So at least $f$ restricted to the set $\{0,1,2,3\}$ ia an injection. We prove that $f(x)=f(y) \Longrightarrow x=y$, for $x, y<k$ implies $f(x)=f(y) \Longrightarrow x=y$, for $x, y<2 k$. So assume $x$ and $y$ are smaller than $2 k$ and $f(x)=f(y)$. If $f(x)$ is even, then $x=2 t, y=2 u$, and $2 f(t)=2 f(u)$. As $t$ and $u$ are less than $k$, we have $t=u$, and $x=y$. Assume $f(x) \equiv 1 \bmod 4$. Then $x \equiv 3 \bmod 4 ;$ $x=4 u-1$, and $f(x)=2 f(2 u-1)-1$. Also $y=4 t-1$ and $f(y)=2 f(2 t-1)-1$. Moreover, $2 u-1<\frac{1}{2}(4 u-1)<k$ and $2 t-1<k$, so $2 u-1=2 t-1, u=t$, and $x=y$. If, finally, $f(x) \equiv 3 \bmod 4$, then $x=4 u+1, y=4 t+1, u<k, t<k, 4 f(u)+3=4 f(t)+3, u=t$, and $x=y$. Since for all $x$ and $y$ there is an $n$ such that the larger one of the numbers $x$ and $y$ is $<2^{n} \cdot 3$, the induction argument above shows that $f(x)=f(y) \Rightarrow x=y$.
|
proof
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 402
|
98.1. Determine all functions $f$ defined in the set of rational numbers and taking their values in the same set such that the equation $f(x+y)+f(x-y)=2 f(x)+2 f(y)$ holds for all rational numbers $x$ and $y$.
|
Solution. Insert $x=y=0$ in the equation to obtain $2 f(0)=4 f(0)$, which implies $f(0)=0$. Setting $x=0$, one obtains $f(y)+f(-y)=2 f(y)$ of $f(-y)=f(y)$. Then assume $y=n x$, where $n$ is a positive integer. We obtain
$$
f((n+1) x)=2 f(x)+2 f(n x)-f((n-1) x)
$$
In particular, $f(2 x)=2 f(x)+2 f(x)-f(0)=4 f(x)$ and $f(3 x)=2 f(x)+2 f(2 x)-f(x)=$ $9 f(x)$. We prove $f(n x)=n^{2} f(x)$ for all positive integers $n$. This is true for $n=1$. Assume $f(k x)=k^{2} f(x)$ for $k \leq n$. Then
$$
\begin{aligned}
& f((n+1) x)=2 f(x)+2 f(n x)-f((n-1) x) \\
& =\left(2+2 n^{2}-(n-1)^{2}\right) f(x)=(n+1)^{2} f(x)
\end{aligned}
$$
and we are done. If $x=1 / q$, where $q$ is a positive integer, $f(1)=f(q x)=q^{2} f(x)$. So $f(1 / q)=f(1) / q^{2}$. This again implies $f(p / q)=p^{2} f(1 / q)=(p / q)^{2} f(1)$. We have shown that there is a rational number $a=f(1)$ such that $f(x)=a x^{2}$ for all positive rational numbers $x$. But since $f$ is an even function, $f(x)=a x^{2}$ for all rational $x$. We still have to check that for every rational $a, f(x)=a x^{2}$ satisfies the conditions of the problem. In fact, if $f(x)=a x^{2}$, then $f(x+y)+f(x-y)=a(x+y)^{2}+a(x-y)^{2}=2 a x^{2}+2 a y^{2}=2 f(x)+2 f(y)$. So the required functions are all functions $f(x)=a x^{2}$ where $a$ is any rational number.
|
f(x)=^{2}
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 403
|
98.2. Let $C_{1}$ and $C_{2}$ be two circles intersecting at $A$ and $B$. Let $S$ and $T$ be the centres of $C_{1}$ and $C_{2}$, respectively. Let $P$ be a point on the segment $A B$ such that $|A P| \neq|B P|$ and $P \neq A, P \neq B$. We draw a line perpendicular to $S P$ through $P$ and denote by $C$ and $D$ the points at which this line intersects $C_{1}$. We likewise draw a line perpendicular to TP through $P$ and denote by $E$ and $F$ the points at which this line intersects $C_{2}$. Show that $C, D, E$, and $F$ are the vertices of a rectangle.
|
Solution. (See Figure 10.) The power of the point $P$ with respect to the circles $C_{1}$ and $C_{2}$ is $P A \cdot P B=P C \cdot P D=P E \cdot P F$. Since $S P$ is perpendicular to the chord $C D, P$
Figure 10 .
has to be the midpoint of $C D$. So $P C=P D$. In a similar manner, we obtain $P E=P F$. Alltogether $P C=P D=P E=P F=\sqrt{P A \cdot P B}$. Consequently the points $C, D, E$, and $F$ all lie on a circle withe center $P$, and $C D$ and $E F$ as diameters. By Thales' theorem, the angles $\angle E C F, \angle C F D$ etc. are right angles. So $C D E F$ is a rectangle.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 404
|
98.3. (a) For which positive numbers $n$ does there exist a sequence $x_{1}, x_{2}, \ldots, x_{n}$, which contains each of the numbers 1, 2, ..., $n$ exactly once and for which $x_{1}+x_{2}+\cdots+x_{k}$ is divisible by $k$ for each $k=1,2, \ldots, n$ ?
(b) Does there exist an infinite sequence $x_{1}, x_{2}, x_{3}, \ldots$, which contains every positive integer exactly once and such that $x_{1}+x_{2}+\cdots+x_{k}$ is divisible by $k$ for every positive integer $k$ ?
|
Solution. (a) We assume that $x_{1}, \ldots, x_{n}$ is the sequence required in the problem. Then $x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}$. This sum should be divisible by $n$. If $n$ is odd, this is possible, since $\frac{(n+1)}{2}$ is an integer. If, on the other hand, $n=2 m$, then $\frac{n(n+1)}{2}=m(2 m+1)=$ $2 m^{2}+m \equiv m \bmod 2 m$. So even $n$ 's are ruled out. Assume $n=2 m+1>1$. We require that $n-1=2 m$ divides evenly the number $x_{1}+\cdots+x_{n-1}$. Since $x_{1}+\cdots+x_{n-1}=$ $(m+1)(2 m+1)-x_{n} \equiv m+1-x_{n} \bmod 2 m$, and $1 \leq x_{n} \leq n$, we must have $x_{n}=m+1$. We also require that $n-2=2 m-1$ divides evenly the number $x_{1}+\cdots+x_{n-2}$. Now $x_{1}+\cdots+x_{n-2}=(m+1)(2 m+1)-x_{n}-x_{n-1} \equiv m+1-x_{n-1} \bmod (2 m-1)$ and $-m \leq m+1-x_{n-1} \leq m$, we have $x_{n-1}=m+1 \bmod (2 m-1)$. If $n>3$ or $m \geq 1$, we must have $x_{n-1}=m+1=x_{n}$, which is not allowed. So the only possibilities are $n=1$ or $n=3$. If $n=1, x_{1}=1$ is a possible sequence. If $n=3$, we must have $x_{3}=2 . x_{1}$ and $x_{2}$ are 1 and 3 in any order.
(b) Let $x_{1}=1$. We define the sequence by a recursion formula. Assume that $x_{1}, x_{2}, \ldots, x_{n-1}$ have been chosen and that the sum of these numbers is $A$. Let $m$ be the smallest integer not yet chosen into the sequence. If $x_{n+1}$ is chosen to be $m$, there will be two restrictions on $x_{n}$ :
$$
A+x_{n} \equiv 0 \bmod n \quad \text { and } \quad A+x_{n}+m \equiv 0 \bmod n+1
$$
Since $n$ and $n+1$ are relatively prime, there exists, by the Chinese Remainder Theorem, a $y$ such that $y \equiv-A \bmod n$ and $y \equiv-A-m \bmod n+1$. If one adds a suitably large
multiple of $n(n+1)$ to $y$, one obtains a number not yet in the sequence. So the sequence always can be extended by two numbers, and eventually every positive integer will be included.
|
notfound
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 405
|
98.4. Let $n$ be a positive integer. Count the number of numbers $k \in\{0,1,2, \ldots, n\}$ such that $\binom{n}{k}$ is odd. Show that this number is a power of two, i.e. of the form $2^{p}$ for some nonnegative integer $p$.
|
Solution. The number of odd binomial coefficients $\binom{n}{k}$ equals the number of ones on the $n$ :th line of the Pascal Triangle $\bmod 2$ :

(We count the lines so that the uppermost line is line 0 ). We notice that line 1 has two copies of line 0 , lines 2 and 3 contain two copies of lines 1 and 2 , etc.
The fundamental property $\binom{n+1}{p}=\binom{n}{p-1}+\binom{n}{p}$ of the Pascal Triangle implies that if all numbers on line $k$ are $\equiv 1 \bmod 2$, then on line $k+1$ exactly the first and last numbers are $\equiv 1 \bmod 2$. If, say on line $k$ exactly the first and last numbers are $\equiv 1 \bmod 2$, then the lines $k, k+1, \ldots, 2 k-1$ are formed by two copies of lines $0,1, \ldots k-1$, separated by zeroes. As line 0 has number 1 and line 1 is formed by two ones, the lines 2 and three are formed by two copies of lines 0 and 1 , etc. By induction we infer that for every $k$, the line $2^{k}-1$ is forned of ones only - it has two copies of line $2^{k-1}-1$, and the line $0=2^{0}-1$ is a one. The line $2^{k}$ has ones in the end and zeroes in between. Now let $N_{n}$ be the number of ones on line $n=2^{k}+m, m<2^{k}$. Then $N_{1}=2$ and $N_{n}=2 N_{m}$. So $N_{n}$ always is a power of two. To be more precise, we show that $N_{n}=2^{e(n)}$, where $e(n)$ is the number of ones in the binary representation of $n$. The formula is true for $n=0$, as $N_{0}=1=2^{e(0)}$. Also, if $m<2^{k}, e\left(2^{k}+m\right)=e(m)+1$. On the other hand, if $n=2^{k}+m, m<2^{k}$ then $N_{n}=2 N_{m}=2 \cdot 2^{e(m)}=2^{e(m)+1}=2^{e(n)}$.
|
2^{e(n)}
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 406
|
99.1. The function $f$ is defined for non-negative integers and satisfies the condition
$$
f(n)= \begin{cases}f(f(n+11)), & \text { if } n \leq 1999 \\ n-5, & \text { if } n>1999\end{cases}
$$
Find all solutions of the equation $f(n)=1999$.
|
Solution. If $n \geq 2005$, then $f(n)=n-5 \geq 2000$, and the equation $f(n)=1999$ has no solutions. Let $1 \leq k \leq 4$. Then
$$
\begin{gathered}
2000-k=f(2005-k)=f(f(2010-k)) \\
=f(1999-k)=f(f(2004-k))=f(1993-k)
\end{gathered}
$$
Let $k=1$. We obtain three solutions $1999=f(2004)=f(1998)=f(1992)$. Moreover, $1995=f(2000)=f(f(2005))=f(1994)$ and $f(1993)=f(f(2004))=f(1999)=$ $f(f(2010))=f(2005)=2000$. So we have shown that $2000-k=f(1999-k)$, for $k=0,1,2,3,4,5$, and $2000-k=f(1993-k)$ for $k=0,1,2,3,4$. We now show by downwards induction that $f(6 n+1-k)=2000-k$ for $n \leq 333$ and $0 \leq k \leq 5$. This has already been proved for $n=333$ and $n=332$. We assume that the claim is true for $n=m+2$ and $n=m+1$. Then $f(6 m+1-k)=f(f(6 m+12-k))=$ $f(f(6(m+2)+1-(k+1))=f(2000-k-1)=f(1999-k)=2000-k$ for $k=0,1,2,3,4$, and $f(6 m+1-5)=f(6 m-4)=f(f(6 m+7))=f(f(6(m+1)+1))=f(2000)=1995=2000-5$. So the claim is true for $n=m$. Summing up, $1999=2000-1=f(6 n)$, if and only if $n=1,2, \ldots, 334$.
|
1999=f(6n),ifonlyifn=1,2,\ldots,334
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 407
|
99.2. Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
Solution. It is easy to give examples of heptagons $A B C D E F G$ inscribed in a circle with all sides unequal and two angles equal to $120^{\circ}$. These angles cannot lie on adjacent vertices of the heptagon. In fact, if $\angle A B C=\angle B C D=120^{\circ}$, and arc $B C$ equals $b^{\circ}$, then arcs $A B$ and $C D$ both are $120^{\circ}-b^{\circ}$ (compute angles in isosceles triangles with center of the circle as the to vertex), and $A B=C D$, contrary to the assumption. So if the heptagon has three angles of $120^{\circ}$, their vertices are, say $A, C$, and $E$. Then each of the arcs $G A B, B C D$, $D E F$ are $360^{\circ}-240^{\circ}=120^{\circ}$. The arcs are disjoint, so they cover the whole circumference. The $F$ has to coincide with $G$, and the heptagon degenerates to a hexagon. There can be at most two $120^{\circ}$ angles.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 408
|
99.3. The infinite integer plane $\mathbb{Z} \times \mathbb{Z}=\mathbb{Z}^{2}$ consists of all number pairs $(x, y)$, where $x$ and $y$ are integers. Let $a$ and $b$ be non-negative integers. We call any move from a point $(x, y)$ to any of the points $(x \pm a, y \pm b)$ or $(x \pm b, y \pm a) a(a, b)$-knight move. Determine all numbers $a$ and $b$, for which it is possible to reach all points of the integer plane from an arbitrary starting point using only $(a, b)$-knight moves.
|
Solution. If the greatest common divisor of $a$ and $b$ is $d$, only points whose coordinates are multiples of $d$ can be reached by a sequence of $(a, b)$-knight moves starting from the origin. So $d=1$ is a necessary condition for the possibility of reaching every point in the integer plane. In any $(a, b)$-knight move, $x+y$ either stays constant or increases or diminishes by $a+b$. If $a+b$ is even, then all points which can be reached from the origin have an even coordinate sum. So $a+b$ has to be odd. We now show that if $d=1$ and $a+b$ is odd, then all points can be reached. We may assume $a \geq 1$ and $b \geq 1$, for if $a b=0, d=1$ is possible only if one of the numbers $a, b$ is 0 and the other one 1 . In this case clearly all points can be reached. Since $d=1$, there exist positive numbers $r$ and $s$ such that either $r a-s b=1$ or $s b-r a=1$. Assume $r a-s b=1$. Make $r$ moves $(x, y) \rightarrow(x+a, y+b)$ and $r$ moves $(x, y) \rightarrow(x+a, y-b)$ to travel from point $(x, y)$ to point $(x+2 r a, y)$. After this, make $s$ moves $(x, y) \rightarrow(x-b, a)$ and $s$ moves $(x, y) \rightarrow(x-b,-a)$ to arrive at point $(x+2 r a-2 s b, y)=(x+2, y)$. In a similar manner we construct sequences of moves carrying us from point $(x, y)$ to points $(x-2, y),(x, y+2)$, and $(x, y-2)$. This means that we can reach all points with both coordinates even from the origin. Exactly one of the numbers $a$ and $b$ is odd. We may assume $a=2 k+1, b=2 m$. A move $(x, y) \rightarrow(x+a, y+b)=(x+1+2 k, y+2 m)$, followed by $k$ sequences of moves
$(x, y) \rightarrow(x-2, y)$ and $m$ sequences of moves $(x, y) \rightarrow(x, y-2)$ takes us to the point $(x+1, y)$. In a similar manner we reach the points $(x-1, y)$ and $(x, y \pm 1)$ from $(x, y)$. So all points can be reached from the origin. - If $s b-r a=1$, the argument is similar.
|
proof
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 409
|
99.4. Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers and $n \geq 1$. Show that
$$
\begin{aligned}
& n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right) \\
& \quad \geq\left(\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}}\right)\left(n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)
\end{aligned}
$$
When does equality hold?
|
Solution. The inequality of the problem can be written as
$$
\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}} \leq \frac{n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)}{n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}}
$$
A small manipulation of the right hand side brings the inequality to the equivalent form
$$
\frac{1}{\frac{1}{a_{1}^{-1}}+1}+\cdots+\frac{1}{\frac{1}{a_{n}^{-1}}+1} \leq \frac{n}{\frac{1}{\frac{a_{1}^{-1}+\cdots+a_{n}^{-1}}{n}}+1}
$$
Consider the function
$$
f(x)=\frac{1}{\frac{1}{x}+1}=\frac{x}{1+x}
$$
We see that it is concave, i.e.
$$
t f(x)+(1-t) f(y)<f(t x+(1-t) y)
$$
for all $t \in(0,1)$. In fact, the inequality
$$
t \frac{x}{1+x}+(1-t) \frac{y}{1+y}<\frac{t x+(1-t) y}{1+t x+(1-t) y}
$$
can be written as
$$
t^{2}(x-y)^{2}<t(x-y)^{2}
$$
and because $0<t<1$, it is true. [Another standard way to see this is to compute
$$
f^{\prime}(x)=\frac{1}{(1+x)^{2}}, \quad f^{\prime \prime}(x)=-\frac{2}{(1+x)^{3}}<0
$$
A function with a positive second derivative is concave.] For any concave function $f$, the inequality
$$
\frac{1}{n}\left(f\left(x_{1}\right)+f\left(x_{2}\right)+\cdots+f\left(x_{n}\right)\right) \leq f\left(\frac{x_{1}+\cdots+x_{n}}{n}\right)
$$
holds, with equality only for $x_{1}=x_{2}=\ldots=x_{n}$. So (1) is true, and equality holds only if all $a_{i}$ 's are equal.
|
proof
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 410
|
00.1. In how many ways can the number 2000 be written as a sum of three positive, not necessarily different integers? (Sums like $1+2+3$ and $3+1+2$ etc. are the same.)
|
Solution. Since 3 is not a factor of 2000 , there has to be at least two different numbers among any three summing up to 2000 . Denote by $x$ the number of such sums with three different summands and by $y$ the number of sums with two different summands. Consider 3999 boxes consequtively numbered fron 1 to 3999 such that all boxes labelled by an odd number contain a red ball. Every way to put two blue balls in the even-numbered boxes produces a partition of 2000 in three summands. There are $\binom{1999}{2}=999 \cdot 1999$ ways to place the blue balls. But htere are $3!=6$ different placements, which produce the same partition of 2000 into three different summands, and $\frac{3!}{2}=3$ different placements, which produce the same partition of 2000 into summands two which are equal. Thus $6 x+3 y=$ 1999.999. But $y=999$, because the number appering twice in the partition can be any of the numbers $1,2, \ldots, 999$. This leads to $x=998 \cdot 333$, so $x+y=1001 \cdot 333=333333$.
|
333333
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 411
|
00.2. The persons $P_{1}, P_{1}, \ldots, P_{n-1}, P_{n}$ sit around a table, in this order, and each one of them has a number of coins. In the start, $P_{1}$ has one coin more than $P_{2}, P_{2}$ has one coin more than $P_{3}$, etc., up to $P_{n-1}$ who has one coin more than $P_{n}$. Now $P_{1}$ gives one coin to $P_{2}$, who in turn gives two coins to $P_{3}$ etc., up to $P_{n}$ who gives $n$ coins to $P_{1}$. Now the process continues in the same way: $P_{1}$ gives $n+1$ coins to $P_{2}, P_{2}$ gives $n+2$ coins to $P_{3}$; in this way the transactions go on until someone has not enough coins, i.e. a person no more can give away one coin more than he just received. At the moment when the process comes to an end in this manner, it turns out that there are to neighbours at the table such that one of them has exactly five times as many coins as the other. Determine the number of persons and the number of coins circulating around the table.
|
Solution. Assume that $P_{n}$ has $m$ coins in the start. Then $P_{n-1}$ has $m+1$ coins, ... and $P_{1}$ has $m+n-1$ coins. In every move a player receives $k$ coins and gives $k+1$ coins away, so her net loss is one coin. After the first round, when $P_{n}$ has given $n$ coins to $P_{1}$, $P_{n}$ has $m-1$ coins, $P_{n-1}$ has $m$ coins etc., after two rounds $P_{n}$ has $m-2$ coins, $P_{n-1}$ has $m-1$ coins etc. This can go on during $m$ rounds, after which $P_{n}$ has no money, $P_{n-1}$ has one coin etc. On round $m+1$ each player still in possession of money can receive and give away coins as before. The penniless $P_{n}$ can no more give away coins according to the rule. She receives $n(m+1)-1$ coins from $P_{n-1}$, but is unable to give $n(m+1)$ coins to $P_{1}$. So when the game ends, $P_{n-1}$ has no coins and $P_{1}$ has $n-2$ coins. The only pair of neighbours such that one has 5 times as many coins as the other can be $\left(P_{1}, P_{n}\right)$. Because $n-21$, the possibilities are $n=3, m=1$ or $n=9, m=3$. Both are indeed possible. In the first case the number of coins is $3+2+1=6$, in the second $11+10+\cdots+3=63$.
|
6or63
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 412
|
00.3. In the triangle $A B C$, the bisector of angle $B$ meets $A C$ at $D$ and the bisector of angle $C$ meets $A B$ at $E$. The bisectors meet each other at $O$. Furthermore, $O D=O E$. Prove that either $A B C$ is isosceles or $\angle B A C=60^{\circ}$.
|
Solution. (See Figure 11.) Consider the triangles $A O E$ and $A O D$. They have two equal pairs of sides and the angles facing one of these pairs are equal. Then either $A O E$ and $A O D$ are congruent or $\angle A E O=180^{\circ}-\angle A D O$. In the first case, $\angle B E O=\angle C D O$, and
Figure 11.
the triangles $E B O$ and $D C O$ are congruent. Then $A B=A C$, and $A B C$ is isosceles. In the second case, denote the angles of $A B C$ by $2 \alpha, 2 \beta$, and $2 \gamma$, and the angle $A E O$ by $\delta$. By the theorem on the adjacent angle of an angle of a triangle, $\angle B O E=\angle D O C=\beta+\gamma$, $\delta=2 \beta+\gamma$, and $180^{\circ}-\delta=\beta+2 \gamma$. Adding these equations yields $3(\beta+\gamma)=180^{\circ}$ eli $\beta+\gamma=60^{\circ}$. Combining this with $2(\alpha+\beta+\gamma)=180^{\circ}$, we obtain $2 \alpha=60^{\circ}$.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 413
|
00.4. The real-valued function $f$ is defined for $0 \leq x \leq 1, f(0)=0, f(1)=1$, and
$$
\frac{1}{2} \leq \frac{f(z)-f(y)}{f(y)-f(x)} \leq 2
$$
for all $0 \leq x<y<z \leq 1$ with $z-y=y-x$. Prove that
$$
\frac{1}{7} \leq f\left(\frac{1}{3}\right) \leq \frac{4}{7}
$$
|
Solution. We set $f\left(\frac{1}{3}\right)=a$ and $f\left(\frac{2}{3}\right)=b$. Applying the inequality of the problem for $x=\frac{1}{3}, y=\frac{2}{3}$ and $z=1$, as well as for $x=0, y=\frac{1}{3}$, and $z=\frac{2}{3}$, we obtain
$$
\frac{1}{2} \leq \frac{1-b}{b-a} \leq 2, \quad \frac{1}{2} \leq \frac{b-a}{a} \leq 2
$$
If $a1$. A similar contradiction would be implied by the assumption $b-a0$ and $b-a>0$, so
$$
\frac{1}{3}\left(\frac{2}{3} a+\frac{1}{3}\right) \leq a \leq \frac{2}{3}\left(\frac{1}{3} a+\frac{2}{3}\right)
$$
or $a \leq 2 b-2 a, b-a \leq 2 a, b-a \leq 2-2 b$, and $1-b \leq 2 b-2 a$. Of these inequalities the first and third imply $3 a \leq 2 b$ and $3 b \leq 2+a$. Eliminate $b$ to obtain $3 a \leq \frac{4}{3}+\frac{2 a}{3}$, $a \leq \frac{4}{7}$. In a corresponding manner, the second and fourth inequality imply $1+2 a \leq 3 b$
and $b \leq 3 a$, from which $1 \leq 7 a$ or $\frac{1}{7} \leq a$ follows. [The bounds can be improved. In fact the sharp lower and upper bounds for $a$ are known to be $\frac{4}{27}$ and $\frac{76}{135}$.]
|
\frac{1}{7}\leq\leq\frac{4}{7}
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 414
|
01.1. Let $A$ be a finite collection of squares in the coordinate plane such that the vertices of all squares that belong to $A$ are $(m, n),(m+1, n),(m, n+1)$, and $(m+1, n+1)$ for some integers $m$ and $n$. Show that there exists a subcollection $B$ of $A$ such that $B$ contains at least $25 \%$ of the squares in $A$, but no two of the squares in $B$ have a common vertex.
|
Solution. Divide the plane into two sets by painting the strips of squares parallel to the $y$ axis alternately red and green. Denote the sets of red and green squares by $R$ and $G$, respectively. Of the sets $A \cap R$ and $A \cap G$ at least one contains at least one half of the squares in $A$. Denote this set by $A_{1}$. Next partition the strips of squares which contain squares of $A_{1}$ into two sets $E$ and $F$ so that each set contains every second square of $A_{1}$ on each strip. Now neither of the dets $E$ and $F$ has a common point with a square in the same set. On the other hand, at least one of the sets $E \cap A_{1}, F \cap A_{1}$ contains at least one half of the squares in $A_{1}$ and thus at least one quarter of the sets in $A$. This set is good for the required set $B$.
|
proof
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 415
|
01.2. Let $f$ be a bounded real function defined for all real numbers and satisfying for all real numbers $x$ the condition
$$
f\left(x+\frac{1}{3}\right)+f\left(x+\frac{1}{2}\right)=f(x)+f\left(x+\frac{5}{6}\right)
$$
Show that $f$ is periodic. (A function $f$ is bounded, if there exists a number $L$ such that $|f(x)|<L$ for all real numbers $x$. A function $f$ is periodic, if there exists a positive number $k$ such that $f(x+k)=f(x)$ for all real numbers $x$.)
|
Solution. Let $g(6 x)=f(x)$. Then $g$ is bounded, and
$$
\begin{gathered}
g(t+2)=f\left(\frac{t}{6}+\frac{1}{3}\right), \quad g(t+3)=f\left(\frac{t}{6}+\frac{1}{2}\right) \\
g(t+5)=f\left(\frac{t}{6}+\frac{5}{6}\right), \quad g(t+2)+g(t+3)=g(t)+g(t+5) \\
g(t+5)-g(t+3)=g(t+2)-g(t)
\end{gathered}
$$
for all real numbers $t$. But then
$$
\begin{gathered}
g(t+12)-g(6) \\
=g(t+12)-g(t+10)+g(t+10)-g(t+8)+g(t+8)-g(t+6) \\
=g(t+9)-g(t+7)+g(t+7)-g(t+5)+g(t+5)-g(t+3) \\
=g(t+6)-g(t+4)+g(t+4)-g(t+2)+g(t+2)-g(t) \\
=g(t+6)-g(t)
\end{gathered}
$$
By induction, then $g(t+6 n)-g(t)=n(g(t+6)-g(0))$ for all positive integers $n$. Unless $g(t+6)-g(t)=0$ for all real $t, g$ cannot be bounded. So $g$ has to be periodic with 6 as a period, whence $f$ is periodic, with 1 as a period.
|
proof
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 416
|
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
Solution. Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 417
|
01.4. Let $A B C D E F$ be a convex hexagon, in which each of the diagonals $A D, B E$, and $C F$ divides the hexagon in two quadrilaterals of equal area. Show that $A D, B E$, and $C F$ are concurrent.
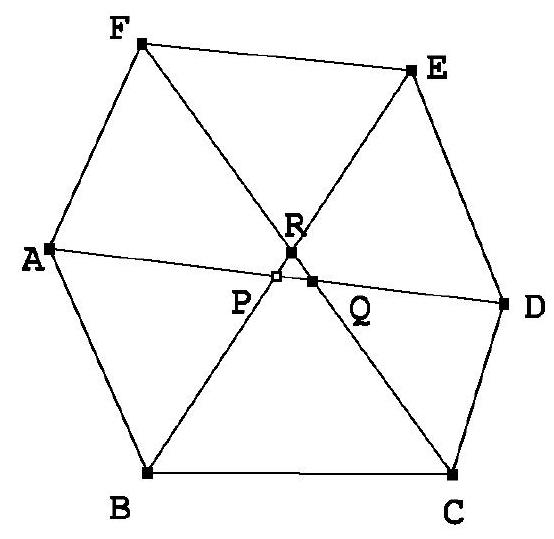
Figure 12.
|
Solution. (See Figure 12.) Denote the area of a figure by $|\cdot|$. Let $A D$ and $B E$ intersect at $P, A D$ and $C F$ at $Q$, and $B E$ and $C F$ at $R$. Assume that $P, Q$, and $R$ are different. We may assume that $P$ lies between $B$ and $R$, and $Q$ lies between $C$ and $R$. Both $|A B P|$ and $|D E P|$ differ from $\frac{1}{2}|A B C D E F|$ by $|B C D P|$. Thus $A B P$ and $D E P$ have equal area. Since $\angle A P B=\angle D P E$, we have $A P \cdot B P=D P \cdot E P=(D Q+Q P)(E R+R P)$. Likewise $C Q \cdot D Q=(A P+P Q)(F R+R Q)$ and $E R \cdot F R=(C Q+Q R)(B P+P R)$. When we multiply the three previous equalities, we obtain $A P \cdot B P \cdot C Q \cdot D Q \cdot E R \cdot F R=$ $D Q \cdot E R \cdot A P \cdot F R \cdot C Q \cdot B P+$ positive terms containing $P Q, Q R$, and $P R$. This is a contradiction. So $P, Q$ and $R$ must coincide.
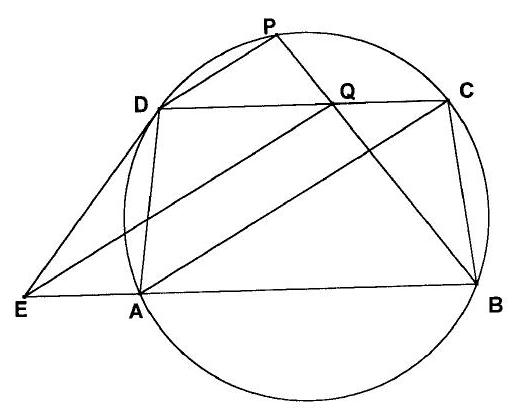
Figure 13.
|
proof
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 418
|
02.1. The trapezium $A B C D$, where $A B$ and $C D$ are parallel and $A D<C D$, is inscribed in the circle c. Let DP be a chord of the circle, parallel to AC. Assume that the tangent to $c$ at $D$ meets the line $A B$ at $E$ and that $P B$ and $D C$ meet at $Q$. Show that $E Q=A C$.
|
Solution. (See Figure 13.) since $A D<C D, \angle P D C=\angle D C A<\angle D A C$. This implies that arc $C P$ is smaller than arc $C D$, and $P$ lies on that arc $C D$ which does not include $A$ and $B$. We show that the triangles $A D E$ and $C B Q$ are congruent. As a trapezium inscribed in a circle, $A B C D$ is isosceles (because $A B \| C D, \angle B A C=\angle D C A$, hence $B C=$ $A D)$. Because $D P \| A C, \angle P D C=\angle C A B$. But $\angle E D A=\angle C A B$ (angles subtending equal arcs) and $\angle P B C=\angle P D C$ (by the same argument). So $\angle E D A=\angle Q B C$. Because $A B C D$ is an inscribed quadrilateral, $\angle E A D=180^{\circ}-\angle D A B=\angle D C B$. So $\angle E A D=$ $\angle Q C B$. The triangles $A D E$ and $C B Q$ are congruent (asa). But then $E A=Q C$. As, in addition, $E A \| Q C, E A C Q$ is a parallelogram. And so $A C=E Q$, as opposite sides of a parallelogram.
|
AC=EQ
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 419
|
02.2. In two bowls there are in total $N$ balls, numbered from 1 to $N$. One ball is moved from one of the bowls to the other. The average of the numbers in the bowls is increased in both of the bowls by the same amount, $x$. Determine the largest possible value of $x$.
|
Solution. Consider the situation before the ball is moved from urn one to urn two. Let the number of balls in urn one be $n$, and let the sum of numbers in the balls in that urn be $a$. The number of balls in urn two is $m$ and the sum of numbers $b$. If $q$ is the number written in the ball which was moved, the conditions of the problem imply
$$
\left\{\begin{array}{l}
\frac{a-q}{n-1}=\frac{a}{n}+x \\
\frac{b+q}{m+1}=\frac{b}{m}+x
\end{array}\right.
$$
or
$$
\left\{\begin{array}{l}
a=n q+n(n-1) x \\
b=m q-m(m+1) x
\end{array}\right.
$$
Because $n+m=N$ and $a+b=\frac{1}{2} N(N+1)$, we obtain
$$
\frac{1}{2} N(N+1)=N q+x\left(n^{2}-m^{2}-N\right)=N q+x N(n-m-1)
$$
and $q=\frac{1}{2}(N+1)-x(n-m-1), b=\frac{1}{2} m(N+1)-x m n$. But $b \geq 1+2+\cdots+m=\frac{1}{2} m(m+1)$. So $\frac{1}{2}(N+1)-x n=\frac{1}{2}(m+n+1)-x n \geq \frac{1}{2}(m+1)$ or $\frac{n}{2}-x n \geq 0$. Hence $x \leq \frac{1}{2}$. The inequality is sharp or $x=\frac{1}{2}$, when the nubers in the balls in urn one are $m+1, m+2$, $\ldots, N$, the numbers in urn two are $1,2, \ldots, m$, and $q=m+1$.
|
\frac{1}{2}
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 420
|
02.3. Let $a_{1}, a_{2}, \ldots, a_{n}$, and $b_{1}, b_{2}, \ldots, b_{n}$ be real numbers, and let $a_{1}, a_{2}, \ldots, a_{n}$ be all different.. Show that if all the products
$$
\left(a_{i}+b_{1}\right)\left(a_{i}+b_{2}\right) \cdots\left(a_{i}+b_{n}\right)
$$
$i=1,2, \ldots, n$, are equal, then the products
$$
\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
$$
$j=1,2, \ldots, n$, are equal, too.
|
Solution. Let $P(x)=\left(x+b_{1}\right)\left(x+b_{2}\right) \cdots\left(x+b_{n}\right)$. Let $P\left(a_{1}\right)=P\left(a_{2}\right)=\ldots=P\left(a_{n}\right)=d$. Thus $a_{1}, a_{2}, \ldots, a_{n}$ are the roots of the $n$ :th degree polynomial equation $P(x)-d=0$. Then $P(x)-d=c\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)$. Clearly the $n$ :th degree terms of $P(x)$ and $P(x)-d$ are equal. So $c=1$. But $P\left(-b_{j}\right)=0$ for each $b_{j}$. Thus for every $j$,
$$
\begin{gathered}
-d=\left(-b_{j}-a_{1}\right)\left(-b_{j}-a_{2}\right) \cdots\left(-b_{j}-a_{n}\right) \\
=(-1)^{n}\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
\end{gathered}
$$
and the claim follows.
|
proof
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 421
|
02.4. Eva, Per and Anna play with their pocket calculators. They choose different integers and check, whether or not they are divisible by 11. They only look at nine-digit numbers consisting of all the digits 1, 2, .., 9. Anna claims that the probability of such a number to be a multiple of 11 is exactly 1/11. Eva has a different opinion: she thinks the probability is less than $1 / 11$. Per thinks the probability is more than $1 / 11$. Who is correct?
|
Solution. We write the numbers in consideration, $n=a_{0}+10 a_{1}+10^{2} a_{2}+\cdots+10^{8} a_{8}$, in the form
$$
\begin{gathered}
a_{0}+(11-1) a_{1}+(99+1) a_{2}+(1001-1) a_{3} \\
+(9999+1) a_{4}+(100001-1) a_{5}+(999999+1) a_{6} \\
\quad+(10000001-1) a_{7}+(99999999+1) a_{8} \\
=\left(a_{0}-a_{1}+a_{2}-a_{3}+a_{4}-a_{5}+a_{6}-a_{7}+a_{8}\right)+11 k \\
=\left(a_{0}+a_{1}+\cdots+a_{8}\right)-2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)+11 k \\
=44+1+11 k-2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)
\end{gathered}
$$
So $n$ is divisible by 11 if and only if $2\left(a_{1}+a_{3}+a_{5}+a_{7}\right)-1$ is divisible by 11 . Let $s=a_{1}+a_{3}+a_{5}+a_{7}$. Then $1+2+3+4=10 \leq s \leq 6+7+8+9=30$ and $19 \leq 2 s-1 \leq 59$. The only multiples of 11 in the desired interval are 33 and 55 , so $s=17$
or $s=28$. If $s=17$, the smallest number in the set $A=\left\{a_{1}, a_{3}, a_{5}, a_{7}\right\}$ is either 1 or 2 $(3+4+5+6=18)$. Checking the cases, we see that there are 9 possible sets $A:\{2,4,5,6\}$, $\{2,3,5,7\},\{2,3,4,8\},\{1,4,5,7\},\{1,3,6,7\},\{1,3,5,8\},\{1,3,4,9\},\{1,2,6,8\}$, and $\{1,2,5,9\}$. If $s=28$, the largest number in $A$ is $9(5+6+7+8=26)$ and the second largest $8(5+6+7+9=27)$. The only possible $A$ 's are $\{4,7,8,9\}$ and $\{5,6,8,9\}$. The number of different ways to choose the set $A$ is $\binom{9}{4}=\frac{9 \cdot 8 \cdot 7 \cdot 6}{2 \cdot 3 \cdot 4}=126$. Of these, the number of choices leading to a number which is a multiple of 11 is $9+2=11$. This means that the probability of picking a number which is divisible by 11 is $\frac{11}{126}<\frac{11}{121}=\frac{1}{11}$. So Eva's opinion is correct.
|
\frac{11}{126}<\frac{1}{11}
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 422
|
03.1. Stones are placed on the squares of a chessboard having 10 rows and 14 columns. There is an odd number of stones on each row and each column. The squares are coloured black and white in the usual fashion. Show that the number of stones on black squares is even. Note that there can be more than one stone on a square.
|
Solution. Changing the order of rows or columns does not influence the number of stones on a row, on a column or on black squares. Thus we can order the rows and columns in such a way that the $5 \times 7$ rectangles in the upper left and lower right corner are black and the other two $5 \times 7$ rectangles are white. If the number of stones on black squares would be odd, then one of the black rectangles would have an odd number of stones while the number of stones on the other would be even. Since the number of stones is even, one of the white rectangles would have an odd number of stones and the other an even number. But this would imply either a set of five rows or a set of seven columns with an even number of stones. But this is not possible, because every row and column has an odd number of stones. So the number of stones on black squares has to be even.
|
proof
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
| 423
|
03.2. Find all triples of integers $(x, y, z)$ satisfying
$$
x^{3}+y^{3}+z^{3}-3 x y z=2003
$$
|
Solution. It is a well-known fact (which can be rediscovered e.g. by noticing that the left hand side is a polynomial in $x$ having $-(y+z)$ as a zero) that
$$
\begin{aligned}
& x^{3}+y^{3}+z^{3}-3 x y z=(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right) \\
&=(x+y+z) \frac{(x-y)^{2}+(y-z)^{2}+(z-x)^{2}}{2}
\end{aligned}
$$
The second factor in the right hand side is non-negative. It is not hard to see that 2003 is a prime. So the solutions of the equation either satisfy
$$
\left\{\begin{aligned}
x+y+z & =1 \\
(x-y)^{2}+(y-z)^{2}+(z-x)^{2} & =4006
\end{aligned}\right.
$$
or
$$
\left\{\begin{aligned}
x+y+z & =2003 \\
(x-y)^{2}+(y-z)^{2}+(z-x)^{2} & =2
\end{aligned}\right.
$$
Square numbers are $\equiv 0$ or $\equiv 1 \bmod 3$. So in the first case, exactly two of the squares $(x-y)^{2},(y-z)^{2}$, and $(z-x)^{2}$ are multiples of 3. Clearly this is not possible. So we must have $x+y+z=2003$ and $(x-y)^{2}+(y-z)^{2}+(z-x)^{2}=2$. This is possible if and only if one of the squares is 0 and two are 1's. So two of $x, y, z$ have to be equal and the third must differ by 1 of these. This means that two of the numbers have to be 668 and one 667. A substitution to the original equation shows that this necessary condition is also sufficient.
|
(668,668,667)
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
| 424
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.